Ôn tập đạo hàm 11 là một trong những mục tiêu quan trọng mà các em học sinh cần thực hiện. Bởi vì chương đạo hàm lớp 11 không chỉ xuất hiện ở lớp này, mà lên lớp 12 hay các kỳ thi tốt nghiệp, đại học sẽ còn gặp chúng.
Vậy nên, để có thể ôn tập chương đạo hàm lớp 11 hiệu quả hơn, hãy cùng Wikihoc tìm hiểu rõ hơn ngay trong bài viết sau đây.
Ôn tập đạo hàm 11 với kiến thức cơ bản
Trong bộ môn giải tích toán học tại bậc THPT, các em sẽ được làm quen với chương đạo hàm. Được hiểu cơ bản, đạo hàm chính là việc một đại lượng mô tả sự biến thiên của hàm tại một điểm cụ thể.
Vậy nên, khi ôn tập kiến thức chuyên đề toán học này, các em cần phải nắm vững về định nghĩa, quy tắc, công thức, công thức gần đúng và viết phương trình tiếp tuyến của đường cong. Dưới đây là những phân tích cụ thể:

Các dạng toán đạo hàm cơ bản trong lớp 11
Trong quá trình ôn tập đạo hàm 11, việc xác định được các dạng toán và bài tập đạo hàm liên quan đến nó rất quan trọng. Vậy nên, để giúp các em luyện tập một cách bài bản nhất, dưới đây là tổng hợp những dạng toán và bài tập của mỗi dạng chi tiết:
Dạng toán 1: Định nghĩa và quy tắc tính đạo hàm

Ngoài ra, trong dạng toán này sẽ có nhiều dạng bài tập liên quan như:
Dạng 1. Tính đạo hàm bằng định nghĩa.

Dạng 2. Các quy tắc tính đạo hàm và bảng đạo hàm.

Dạng 3. Bài toán chứng minh, giải phương trình, bất phương trình.

Dạng 4. Đạo hàm của hàm số lượng giác.
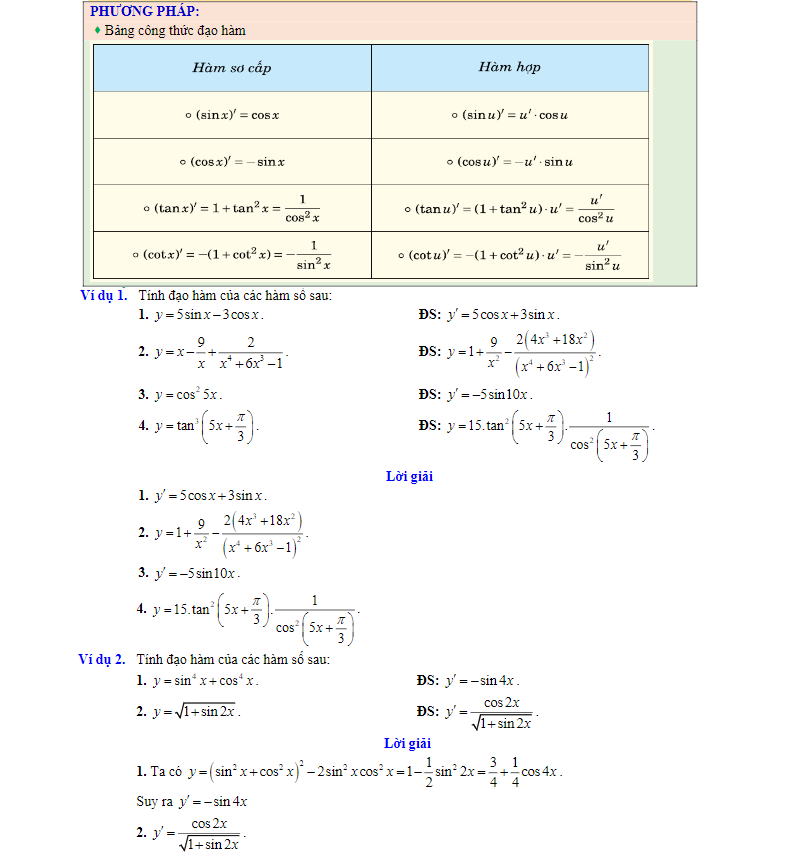
Dạng 5. Chứng minh đẳng thức, giải phương trình chứa đạo hàm.

Dạng toán 2: Phương trình tiếp tuyến của đạo hàm

Ngoài ra, trong dạng toán này sẽ chia ra nhiều dạng bài tập liên quan như sau:
Dạng 1. Viết phương trình tiếp tuyến khi biết tiếp điểm (tại điểm) hoặc biết hoành độ, tung độ.
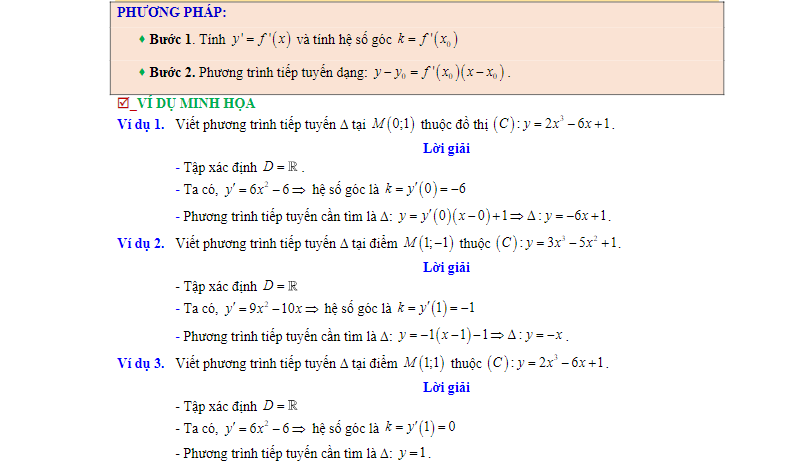
Dạng 2. Viết phương trình tiếp tuyến khi biết hệ số góc hoặc song song, vuông góc với một đường thẳng.

Dạng 3. Bài toán về xác định hệ số góc nhỏ nhất, lớn nhất của tiếp tuyến.

Dạng 4. Viết phương trình tiếp tuyến khi biết điểm mà tiếp tuyến đi qua.

Dạng 5. Tìm tham số để từ một điểm ta kẻ được đúng một tiếp tuyến đến đồ thị hàm số.

Dạng toán 3: Đạo hàm cấp cao và vi phân

Bên cạnh đó, trong dạng toán đạo hàm cao cấp và vi phân này các em cần ôn tập một số dạng bài tập sau đây:
Dạng 1. Tính đạo hàm cấp cao của một hàm số.

Dạng 2. Tìm vi phân của một hàm số.

Bài tập ôn tập đạo hàm 11 từ cơ bản đến nâng cao
Sau khi đã ôn tập xong phần kiến thức cơ bản, lý thuyết trong chương đạo hàm thì dưới đây sẽ là những bài tập liên quan tới các kiến thức trên để các em ôn tập và tự luyện hiệu quả hơn nhé.

Xem thêm: Tất tần tật kiến thức về đạo hàm nhiều biến đầy đủ nhất
Kết luận
Trên đây là tổng hợp những kiến thức về việc ôn tập đạo hàm 11. Về cơ bản, chương đạo hàm lớp 11 không có quá nhiều kiến thức, nhưng các dạng bài tập lại khá nhiều đòi hỏi các em cần phải nắm vững để không bỏ lỡ cơ hội dành điểm trọn vẹn trong các kỳ thi ở chuyên đề này nhé.
