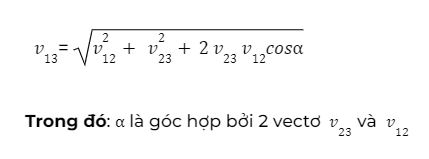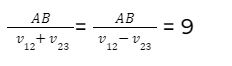Vận tốc là đại lượng quen thuộc và được ứng dụng rất nhiều trong đời sống hằng ngày. Việc tính toán, cộng vận tốc sẽ giúp chúng ta đưa ra một con số tương đối hỗ trợ thực hiện các công việc như di chuyển, lắp đặt, thiết lập máy móc,… một cách dễ dàng hơn. Bài viết sau đây sẽ giúp các em hiểu rõ hơn về công thức cộng vận tốc và các thông tin liên quan đến vận tốc trong chương trình Vật lý lớp 10.
Giải thích tính tương đối của chuyển động
Tính tương đối của quỹ đạo: Hình dạng quỹ đạo của chuyển động trong những hệ quy chiếu khác nhau thì khác nhau. Do đó, ta có thể kết luận quỹ đạo có tính tương đối.
Ví dụ: Khi thời tiết đứng gió, đối với góc nhìn của người đứng bên đường, họ sẽ nhìn thấy giọt mưa rơi theo quỹ đạo là đường thẳng từ trên xuống. Còn đối với người ngồi trên ô tô đang chuyển động, họ sẽ thấy giọt mưa rơi theo phương xiên góc.

Tính tương đối của vận tốc: Vận tốc của một vật chuyển động đối với các hệ qui chiếu khác nhau thì khác nhau. Do đó ta có thể kết luận vận tốc có tính tương đối.
Ví dụ: Xét trường hợp trong một toa tàu, khi hành khách ngồi yên, toa tàu chuyển động với vận tốc 45km/ thì đối với toa tàu, vận tốc của hành khách bằng 0. Đối với người đứng 2 bên đường thì hành khách trên tàu đang chuyển động với vận tốc bằng với vận tốc của toa tàu là 45km/h.
Thế nào là hệ quy chiếu đứng yên và hệ quy chiếu chuyển động?
Hệ quy chiếu đứng yên là hệ quy chiếu gắn với các vật đứng yên.
Hệ quy chiếu chuyển động là hệ quy chiếu gắn với các vật chuyển động
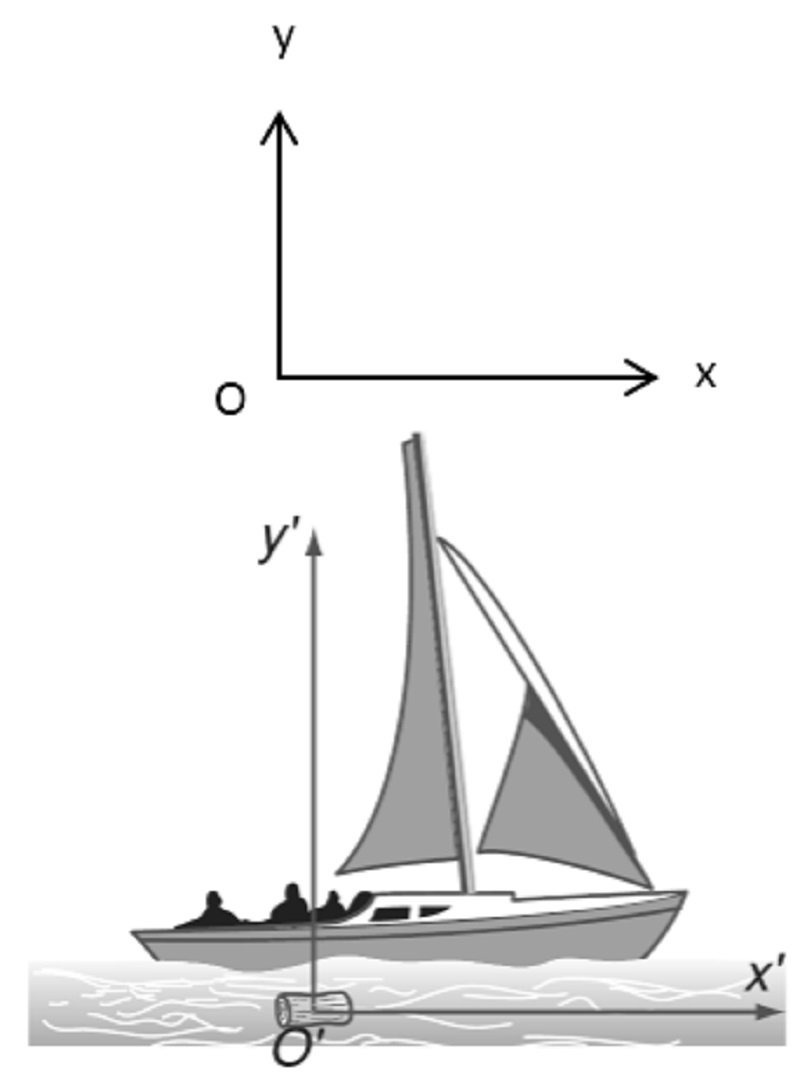
Ví dụ: Một chiếc bè đang chạy trên một dòng sông
-
Gọi (xOy) là hệ quy chiếu đứng yên, gắn với bờ.
-
Gọi (x’O’y’) là hệ quy chiếu chuyển động, gắn với một vật chuyển động (trôi) theo dòng sông.
Công thức cộng vận tốc
Dưới đây là công thức cộng vận tốc dùng để tính vận tốc của các vật trong hệ quy chiếu khác nhau.
Trong đó:
-
Kí hiệu 1 gắn với vật đang xét vận tốc
-
Kí hiệu 2 gắn với hệ quy chiếu các vật chuyển động
-
Kí hiệu 3 gắn với hệ quy chiếu các vật đứng yên
-
v12: là vận tốc của vật được so trong hệ quy chiếu chuyển động. v12 được gọi là vận tốc tương đối
-
v23: là vận tốc của vật được so trong hệ quy chiếu chuyển động so với hệ quy chiếu đứng yên. v23 được gọi là vận tốc kéo theo.
-
v13: là vận tốc của vật so với hệ quy chiếu chuyển động. v13 được gọi là vận tốc tuyệt đối.
Công thức tính độ lớn của vận tốc tuyệt đối:
Trường hợp các vận tốc cùng phương cùng chiều
Công thức tính độ lớn:
Xét về hướng: vectơ v13 cùng hướng với vectơ v12 và v23
Trường hợp vận tốc tương đối cùng phương, ngược chiều với vận tốc kéo theo
Công thức tính độ lớn:
Xét về hướng:
-
Vecto v13 cùng hướng với vectơ v12 khi v12> v23
-
Vecto v13 cùng hướng với vectơ v23 khi v12< v23
Chú ý: Trường hợp vecto v12 vuông góc với vectơ v23 thì:
v12= v122 + v232
Xem thêm: Chuyển động thẳng biến đổi đều là gì? Bao gồm các loại nào? (Vật lý 10)
Bài tập công thức cộng vận tốc
Để giúp các em có thể ghi nhớ công thức và tiếp thu bài một cách hiệu quả hơn, Wikihoc sẽ đưa ra một số bài tập công thức cộng vận tốc cụ thể kèm theo đó là đáp án để các em có thể kiểm tra chính xác sau khi làm.
Câu 1: Nếu một ví dụ về tính tương đối của vận tốc trong chuyển động
Hướng dẫn giải:
Ví dụ về tính tương đối của vận tốc:
Một người ngồi trên xe ô tô đang chuyển động trên đường với vận tốc là 50km/h. Khi đó:
-
Đối với người đứng yên trên vỉa hè thì vận tốc của người ngồi trên ô tô chính bằng vận tốc của ô tô đang chạy là 50km/h
-
Đối với ô tô thì vận tốc của người sẽ bằng không
Câu 2: Một chiếc thuyền chạy ngược dòng sông. Sau 1 giờ thuyền đi được 10km. Một khúc gỗ trôi theo dòng nước sau 1 phút trôi được 100/3m. Cho biết vận tốc của thuyền buồm so với nước bằng bao nhiêu?
Hướng dẫn giải:
Ta có: t1 = 1h = 3600s, S1 = 10km = 10000m, t2 = 1 phút = 60s
Giả sử: thuyền là 1, nước là 2, bờ là 3
Khi đó, ta có:
Độ lớn vận tốc của thuyền so với bờ có giá trị bằng:
v13 = S1/t1 = 10000/36000 = 25/9 (m/s)
Độ lớn vận tốc của nước so với bờ có giá trị bằng:
v23 = S2/t2 = (10/3)/600 = 5/9 (m/s)
Theo công thức cộng vận tốc, ta được: v12= v13+ v32 hay v12= v13- v23
Ta chọn chiều dương là chiều chảy của dòng sông. Theo đề, vì thuyền chạy ngược dòng sông nên v13 hướng ngược chiều dương và v23 hướng theo chiều dương.
Khi đó: v13= -25/9 (m/s) và v23=5/9 (m/s)
v12 = v13 – v23= -30/9 (m/s) = -12 (km/h)
Kết luận: Vậy, vận tốc của thuyền buồm so với dòng nước có độ lớn bằng 12km/h và chuyển động ngược với chiều của dòng nước.
Câu 3: Một chiếc thuyền buồm chuyển động trên đoạn đường AB dài 60km. Vận tốc của thuyền là 15km/h so với dòng nước yên lặng, Tính vận tốc dòng chảy của dòng nước biết thời gian để thuyền đi từ A đến B rồi quay lại A hết 9 giờ.
Hướng dẫn giải:
Phân tích bài toán
-
Gọi: thuyền (1); dòng nước (2); bờ sông (3)
-
Vận tốc của thuyền (1) so với dòng nước (2) v12 = 15km/h
-
Vận tốc của dòng nước (2) so với bờ (3) v23
-
Vận tốc của thuyền (1) so với bờ (3) v13
-
AB=60km
Trường hợp thuyền xuôi theo dòng nước: v13= v12+ v23
Trường hợp thuyền ngược dòng nước: v13= v12- v23
Tổng thời gian đi và về là:
Vậy tính được: v23= 5km/h
Câu 4: Một ca nô đi trong mặt nước yên lặng với vận tốc 16 m/s, vận tốc của dòng nước so với bờ sông là 2 m/s. Góc giữa vectơ vận tốc của ca nô đi trong nước yên lặng và vectơ vận tốc của dòng nước là α (0 < α < 180°). Độ lớn vận tốc của ca nô so với bờ nằm trong khoảng bao nhiêu?
Hướng dẫn giải:
Vận tốc của ca nô so với bờ lớn nhất khi α = 0 => v(max) = 16 + 2 = 18 m/s;
Vận tốc nhỏ nhất khi α = 180°
⟹ v(min) = 16 – 2 = 14 m/s
Do vậy khi 0 < α < 180° thì 14 m/s < v < 18 m/s
Vậy vận tốc của ca nô so với bờ có thể nằm trong khoảng từ 14m/s đến 18m/s
Câu 5: Một chiếc thuyền chuyển động thẳng đều, ngược chiều dòng nước với vận tốc 7 km/h đối với nước. Vận tốc chảy của dòng nước là 1.5 km/h. Vận tốc của thuyền so với bờ bằng bao nhiêu:
Hướng dẫn giải:
Coi thuyền là (t), nước là (n), bờ là (b).
Chọn chiều dương là chiều chuyển động của nước
Vận tốc của thuyền so với nước là: v(tn) = – 7 km/h (do ngược chiều dương)
Vận tốc của nước so với bờ: v(nb) = 1,5 km/h.
Vận tốc của thuyền so với bờ là: v(tb) = -7 +1,5 = -5.5 (km/h) (Áp dụng quy tắc cộng vectơ)
Suy ra độ lớn vận tốc của thuyền so với bờ là 5,5 km/h và chuyển động ngược chiều dòng nước.
Câu 6: Một ô tô A chạy đều trên một đường thẳng với vận tốc 40 km/h. Một ô tô B đuổi theo ô tô A với vận tốc 60 km/h. Xác định vận tốc của ô tô B đối với ô tô A và của ô tô A đối với ô tô B.
Hướng dẫn giải:
Chọn chiều dương là chiều chuyển động của 2 xe
Vecto vAD: vận tốc của xe A đối với đất
Vecto vBD: vận tốc của xe B đối với đất
Vecto vAB: vận tốc của xe B đối với xe A
Vận tốc của xe A đối với xe B: vAB = vAD + vBD hay vAB = vAD – vBD
Vì hai xe chuyển động cùng chiều nên: vAB = 40 – 60 = -20 (km/h) Hướng ngược với chiều dương
Câu 7: Một chiếc thuyền xuôi dòng từ A đến B, vận tốc của dòng nước là 5km/h. Tính vận tốc của thuyền so với dòng nước và chiều dài từ A đến B biết thuyền xuôi dòng mất 2 giờ và ngược dòng mất 3 giờ trên cùng đoạn đường AB.
Hướng dẫn giải:
Phân tích bài toán
-
Gọi: thuyền (1); dòng nước (2); bờ sông (3)
-
Vận tốc của thuyền (1) so với bờ (3): v13
-
Vận tốc của dòng nước (2) so với bờ (3): v23
-
Vận tốc của thuyền (1) so với dòng nước (2): v12
Trường hợp thuyền xuôi theo dòng nước: v13= v12+ v23
Trường hợp thuyền ngược dòng nước: v13= v12- v23
Từ (*) và (**) suy ra: AB = 60km
Câu 8: Trên một tuyến đường xe buýt thẳng, các xe buýt chuyển động theo 1 chiều và cách đều nhau 5km. Một người đi xe đạp chuyển động thẳng đều trên tuyến đường này. Nếu đi theo một chiều thì tại thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h , người này gặp xe buýt thứ 12. Nếu đi theo chiều ngược lại thì thời điểm t=0, người đi xe đạp gặp xe buýt thứ nhất, đến thời điểm t=1h người này gặp xe buýt thứ 6. Hỏi nếu người này đứng yên bên đường thì trong 1 giờ tính từ thời điểm gặp xe buýt thứ nhất, người này còn gặp được bao nhiêu xe buýt nữa ? Bỏ qua kích thước của xe buýt và xe đạp.
Hướng dẫn giải:
Gọi vận tốc của người đi xe đạp so với xe buýt là v12
Gọi vận tốc của xe buýt so với đường là v23
Gọi vận tốc của người đi xe đạp so với đường là v13
Sau 1h gặp xe bus số 12 => Xe đạp chuyển động ngược chiều xe buýt
Sau 1h gặp xe bus số 6 => Xe đạp chuyển động cùng chiều xe buýt
Xe đạp chuyển động ngược chiều với đoàn xe buýt:
v12= v13+ v32 = S/t = (11*5) / 1 = 55 (km)
Người đi xe đạp chuyển động cùng chiều với đoàn xe buýt:
v12= v23- v13 = S/t = 5*5/1 = 25 (km)
Giải hệ phương trình ta được: v23=40km/h
Nếu người đó đứng yên thì số xe buýt đi qua là: 40/5 = 8 (xe)
Lời kết:
Trên đây là bài viết về các kiến thức liên quan đến công thức cộng vận tốc và cách áp dụng công thức vào tính toán các bài tập ở chương trình Vật Lý 10. Hy vọng với các thông tin mà Wikihoc đã đề cập, các em có thể nâng cao khả năng học tập cũng như làm phong phú hơn kiến thức Vật Lý trong quá trình tự tìm hiểu.