Hàm số bậc 2 là một trong các nội dung chính cần học trong chương trình môn toán tại THPT. Nắm bắt được tình hình chung của các bạn học sinh, Wikihoc đã tổng hợp lý thuyết và các dạng bài tập về hàm số bậc hai, giúp bạn dễ dàng ôn tập cũng như ghi nhớ lượng kiến thức này.
Lý thuyết về hàm số bậc 2
Để có thể dễ dàng hoàn thành các bài toán từ cơ bản đến nâng cao của hàm số bậc hai, thì lý thuyết là phần mà các bạn học sinh không thể bỏ qua.
Ôn tập các kiến thức về hàm số
Khái niệm
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x, sao cho mỗi giá trị của x ta luôn xác định một giá trị tương đương y, thì y gọi là hàm số của x, và x được gọi là biến số của y.
Kí hiệu
Hàm số thường được ký hiệu bằng các chữ cái như f, g và h. Có dạng như sau: y = f (x) với cách đọc là “y bằng f của x”, trong đó: x là đối số của hàm y = f (x), và y là giá trị của hàm y = f (x).
Định nghĩa
Cho X, Y là hai tập hợp số, ví dụ là tập hợp số thực, hàm số f xác định trên X, nhận giá trị trong Y là một quy tắc cho tương ứng mỗi số x thuộc X với một số y duy nhất thuộc Y.
Tính chất
-
Khi x thay đổi mà y luôn nhận một giá trị thì y gọi là hàm hằng.
-
Hàm số có thể biểu diễn bằng bảng, bằng công thức toán học.
-
Khi y là hàm số của x thì ta có 3 cách viết sau:
-
f : X → Y
-
f : x → (x)
-
y = f(x)
Trong đó:
-
Tập X gọi là miền xác định.
-
Tập Y gọi là miền giá trị.
-
x gọi là đối số.
-
y là một hàm số.
-
f(x) được gọi là giá trị của hàm f tại x.
Các dạng hàm số
-
Hàm số đơn ánh: Một hàm số là đơn ánh khi nó áp dụng lên 2 đối số khác nhau luôn cho 2 giá trị khác nhau. Có nghĩa là với 2 biến x1 và x2 (x1 # x2) thì f(x1) # f(x2).
-
Hàm số toàn ánh: Hàm số f được gọi là toàn ánh nếu như với mọi số y thuộc Y ta luôn tìm được ít nhất một số x thuộc X sao cho f(x) = y hay y = f(x)
-
Hàm số song ánh: Trong toán học, song ánh, hoặc hàm song ánh, là một hàm số f từ tập X vào tập Y thỏa mãn tính chất, đối với mỗi y thuộc Y, có duy nhất một x thuộc X sao cho f(x) = y.
Hàm số bậc 2 là gì?
- Hàm số bậc hai là hàm số có dạng ax^2 + bx + c trong đó a,b,c là các hằng số và (a # 0). Có tập xác định D = R và biệt thức = b2 – 4ac. Hệ số hoàn toàn có thể ở y. Đồng thời, x và y lần lượt là các biến.
- Trường hợp có 2 biến x và y, hàm số có dạng: f(x,y) = ax^2 + by^2 + cxy + dx + ey + f
Một số thuật ngữ cần nhớ:
-
Hệ số: Hệ số là một nhân tử của một biểu thức trong toán học, một giá trị mà nó xuất hiện phía trước hoặc xuất hiện trong phép nhân với một giá trị khác và thường là một số nhưng không phải biến số.
-
Bậc của hàm: Thuật ngữ “đa thức bậc hai” đôi khi có nghĩa là “có bậc là 2”, hoặc đôi khi là “có bậc cao nhất là 2”. Nếu bậc nhỏ hơn 2, điều này có thể được gọi là “trường hợp suy biến”. Thông thường, nghĩa của thuật ngữ sẽ được xác định bởi ngữ cảnh.
-
Biến: Biến số là một số có giá trị bất kỳ, và có thể thay đổi giá trị trong một tình huống bất kỳ. Một đa thức bậc hai có có 1 biến duy nhất x (trường hợp đơn biến), hoặc nhiều như biến x, y, và z (trường hợp đa biến). Trên thực tế, người ta thường quy một hàm nhiều biến về các hàm 2 biến để dễ xét.
Cách vẽ các dạng đồ thị hàm số bậc 2
Đồ thị của hàm số bậc 2 có dạng như thế nào? Là câu hỏi phổ biến trong các đề thi lớp 9 và lớp 10. Sau đây là cách vẽ các dạng đồ thị hàm số bậc hai mà bạn cần nắm kỹ.
Hàm số bậc hai có dạng y = ax^2
Các bước vẽ đồ thị:
-
Bước 1: Xác định tọa độ của đỉnh (0;0)
-
Bước 2: Xác định khoảng 5 điểm thuộc đồ thị để vẽ đồ thị chính xác hơn.
-
Bước 3: Vẽ parabol
Lưu ý: Khi vẽ parabol cần chú ý đến dấu của hệ số a (a > 0 bề lõm quay lên trên, a < 0 bề lõm quay xuống dưới)
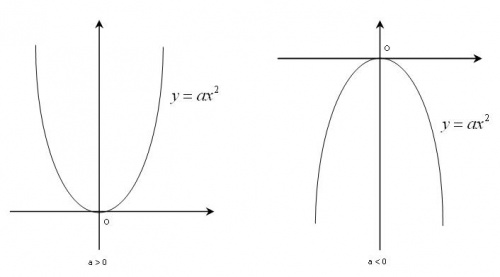
Hàm số bậc hai có dạng y = ax^2+bx+c
Khảo sát hàm số bậc 2
Bảng biến thiên của hàm số y=ax^2+bx+c chia làm 2 trường hợp:
- Trường hợp a > 0, hàm số nghịch biến trên khoảng (−∞ ; −b/2a) và đồng biến trên khoảng (−b/2a ; +∞).
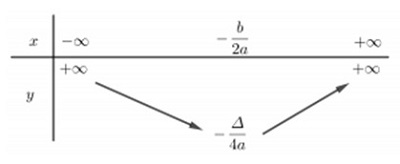
- Trong trường hợp a < 0, hàm số đồng biến trên khoảng (−∞ ; −b/2a) và nghịch biến trên khoảng (−b/2a ; +∞).
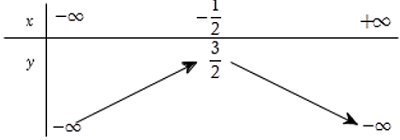
Cách vẽ đồ thị hàm số bậc hai y = ax^2 + bx + c
- Bước 1: Xác định toạ độ đỉnh
- Bước 2: Xác định trục đối xứng x = (-b)/(2a) và hướng bề lõm của parabol.
- Bước 3: Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng).
- Bước 4: Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
Xem thêm: Hàm số tuần hoàn là gì? Cách tính chu kỳ của hàm số lượng giác cực chuẩn
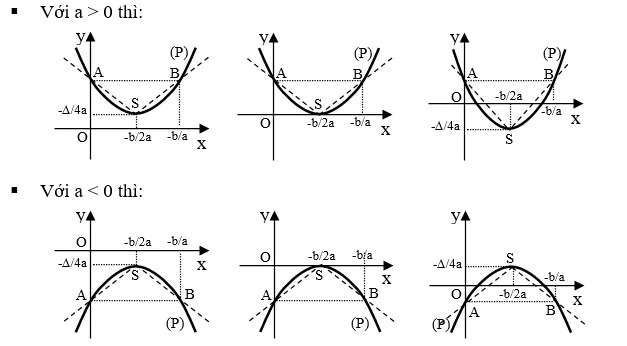
Khảo sát sự biến thiên của hàm số bậc 2
Hàm số bậc 2 đồng biến khi nào?
-
Hàm số f(x) được gọi là đồng biến trên K (K là một khoảng, một đoạn hay nửa đoạn), nếu với mỗi cặp x1, x2 thuộc K mà x1 < x2 thì f(x1) < f(x2).
-
Cho hàm số y = f(x) có đạo hàm f’(x) trên K. Nếu f’(x) >= 0, với mọi x thuộc K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) đồng biến.
Hàm số bậc 2 nghịch biến khi nào?
-
Hàm số f(x) được gọi là nghịch biến trên K (K là một khoảng, một đoạn hay nửa đoạn), nếu với mỗi cặp x1, x2 thuộc K mà x1 < x2 thì f(x1) > f(x2).
-
Cho hàm số y = f(x) có đạo hàm f’(x) trên K. Nếu f’(x) =< 0, với mọi x thuộc K, f’(x) = 0 chỉ tại một số hữu hạn điểm thì f(x) nghịch biến.
Cực trị của hàm số bậc hai là gì?

Cách lập bảng biến thiên của hàm số bậc hai
-
Bước 1: Tìm tập xác định.
-
Bước 2: Tính y′. Tìm các điểm tại đó y′ bằng 0 hoặc không xác định.
-
Bước 3: Lập bảng biến thiên. Từ bảng biến thiên rút ra kết luận.

Một số bài tập xác định hàm số bậc 2 có lời giải
Dưới đây là một số bài toán xác định hàm số bậc 2 có lời giải chi tiết, được Wikihoc sàng lọc và tổng hợp. Và đây cũng là các dạng bài toán thường xuất hiện trong các đề thi lớp 9 và lớp 10, cũng như kỳ thi THPT Toàn Quốc hằng năm.

Trên đây là tất cả nội dung mà Wikihoc muốn chia sẻ với bạn đọc. Hy vọng rằng với những kiến thức về hàm số bậc 2 này, sẽ giúp bạn tự tin hơn trong các kỳ thi sắp tới. Hãy theo dõi chuyên mục “Kiến thức cơ bản” để nhận thêm các thông tin hữu ích sắp tới nhé!
