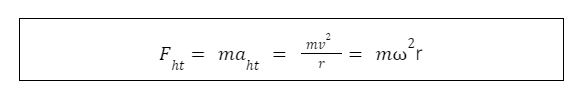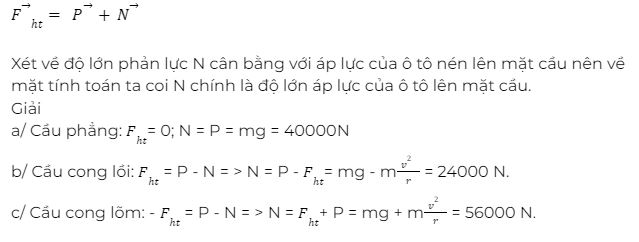Trong chương trình vật lý 10, các em sẽ được tìm hiểu về một loại lực không quá mới lạ nhưng không phải ai cũng hiểu rõ được bản chất của nó, đó là lực hướng tâm. Trong bài viết này, Wikihoc sẽ tổng hợp tất cả các kiến thức xoay quanh lực hướng tâm một cách dễ hiểu nhất. Cùng đọc bài viết dưới đây ngay nhé!
Lực hướng tâm là gì?
Định nghĩa
Lực (hay hợp lực của các lực) tác dụng vào một vật chuyển động tròn đều và gây ra cho vật gia tốc hướng tâm được gọi là lực hướng tâm.
Ví dụ về lực hướng tâm
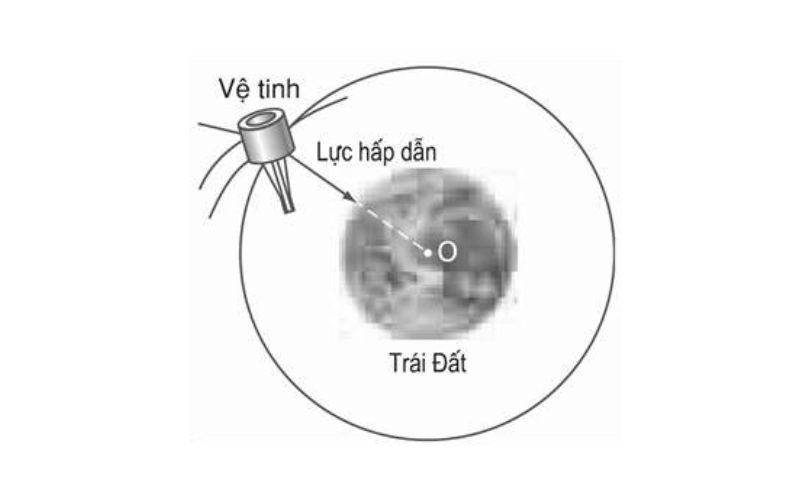
-
Lực hấp dẫn giữa Trái Đất và vệ tinh nhân tạo đóng vai trò lực hướng tâm, giữ cho vệ tinh nhân tạo chuyển động tròn đều xoay quanh Trái Đất
-
Lực căng của dây đã giữ cho vật chuyển động tròn đều, cho thấy lực căng đóng vai trò là lực hướng tâm.
-
Đặt một vật lên trên bàn quay, lực ma sát nghỉ đóng vai trò lực hướng tâm giữ cho vật chuyển động tròn.
-
Đường ôtô và đường sắt ở những đoạn cong cần phải làm nghiêng về phía tâm cong để hợp lực giữa trọng lực và phản lực của mặt đường, tạo ra lực hướng tâm giữ cho xe, tàu chuyển động dễ dàng trên quỹ đạo.
Nguồn gốc lực hướng tâm
Đối với một vệ tinh bay trong quỹ đạo xoay quanh trái đất, lực hướng tâm do lực trọng trường tạo thành giữa vệ tinh và trái đất, tác dụng lực hướng về khối tâm của hai vật. Đối với một vật được gắn vào đầu một sợi dây đang quay theo trục đứng, lực hướng tâm là thành phần nằm ngang của lực căng dây, tác dụng hướng về tâm khối lượng giữa trục quay và vật quay. Đối với một vật đang xoay quanh chính nó, lực căng bên trong là lực hướng tâm giữ cho vật là một khối.
Đặc điểm của lực hướng tâm
Bản chất lực hướng tâm vốn dĩ không phải là một loại lực mới. Lực hướng tâm là hợp lực của các lực tác dụng vào vật, có tác dụng giữ cho vật chuyển động tròn đều và gây ra gia tốc hướng tâm cho vật.
Lực hướng tâm có phương của bán kính quỹ đạo và có chiều hướng vào tâm quay, có điểm đặt tại vật.
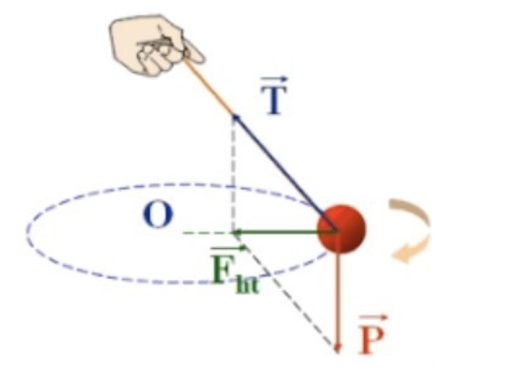
Ví dụ: Hợp lực của lực căng dây và trọng lực
có vai trò lực hướng tâm. Lực này có phương bán kính và có chiều hướng vào tâm quay O.
Công thức lực hướng tâm
Trong đó:
- Fht: là lực hướng tâm (N)
- aht: là gia tốc hướng tâm (m/s2)
- m: là khối lượng của vật (kg)
- r : là bán kính quỹ đạo tròn (m)
- v: là tốc độ dài của vật chuyển động tròn đều (m/s)
- ω: là tốc độ góc của vật chuyển động tròn đều (rad/s)
Ứng dụng của lực hướng tâm
Lực hướng tâm được sử dụng cho máy ly tâm trong phòng thí nghiệm. Tại đây, các hạt lơ lửng trong chất lỏng và được tách ra khỏi chất lỏng bằng các ống gia tốc được định hướng để các hạt nặng hơn bị kéo về phía đáy của các ống.
Lực hướng tâm còn được ứng dụng để tính toán làm đường cong cho đường xe ô tô, đường sắt, giúp tàu xe chuyển động xe dàng.
Ứng dụng trong việc làm vòng quay tại các công viên giải trí,….
Chuyển động li tâm
Chuyển động li tâm là gì?
Khi đặt vật trên bàn quay, nếu bàn quay quá nhanh, lực ma sát nghỉ không đủ lớn để đóng vai trò lực hướng tâm nữa, nên vật sẽ trượt ra xa tâm quay của bàn, và văng khỏi bàn theo phương tiếp tuyến với quỹ đạo. Chuyển động như vậy của vật được gọi là chuyển động ly tâm.
Ứng dụng của chuyển động li tâm
Chuyển động li tâm có rất nhiều ứng dụng trong thực tế, ví dụ điển hình là: Máy vắt li tâm (có thể kể đến như máy giặt ở chế độ vắt, tốc độ quay của lồng giặt lớn làm cho nước văng ra khỏi vải).

Xem thêm: Ánh sáng trắng là gì? Phân biệt ánh sáng trắng và ánh sáng màu
Bài tập lực hướng tâm Lý lớp 10 (có lời giải)
Bài tập 1: Một vật đang chuyển động tròn đều dưới tác dụng của lực hướng tâm F. Nếu bán kính quỹ đạo gấp hai lần so với trước và đồng thời giảm tốc độ quay còn một nửa thì so với ban đầu, lực hướng tâm
A. giảm 8 lần.
B. giảm 4 lần.
C. giảm 2 lần.
D. không thay đổi.
Hướng dẫn giải:
Câu A
Bài tập 2: Một vật nhỏ khối lượng 250 g chuyển động tròn đều trên quỹ đạo bán kính 1,2 m. Biết trong 1 phút vật quay được 120 vòng. Độ lớn lực hướng tâm gây ra chuyển động tròn của vật là
A. 47,3 N.
B. 3,8 N.
C. 4,5 N.
D. 46,4 N.
Hướng dẫn giải:
Câu A
Bài tập 3: Một ô tô có khối lượng 4 tấn chuyển động qua một chiếc cầu lồi có bán kính cong 100 m với tốc độ 72 km/h. Lấy g = 10m/s2. Áp lực của ô tô nén lên cầu khi nó đi qua điểm cao nhất (giữa cầu) là
A. 36000 N.
B. 48000 N.
C. 40000 N.
D. 24000 N.
Hướng dẫn giải:
Câu D
Bài tập 4: Một lò xo có độ cứng 125 N/m, chiều dài tự nhiên 40 cm, một đầu giữ cố định ở A, đầu kia gắn vào quả cầu khối lượng 10 g có thể trượt không ma sát trên thanh nằm ngang. Thanh quay đều quanh trục Δ thẳng đứng với tốc độ 360 vòng/phút. Lấy π2 = 10. Độ giãn của lò xo gần nhất với giá trị nào sau đây?
A. 5,3 cm.
B. 5,0 cm.
C. 5,1 cm.
D. 5,5 cm.
Hướng dẫn giải:
Câu C
Bài tập 5: Tính áp lực của ô tô 4 tấn đi qua điểm giữa cầu với tốc độ 72km/h, lấy g = 10m/s2. Trong các trường hợp sau
a) cầu phẳng.
b) cầu cong lồi bán kính 100m
c) cầu cong lõm bán kính 200 m.
Hướng dẫn giải:
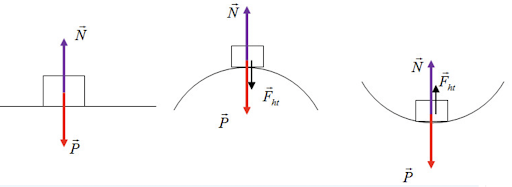
v = 72km/h= 20m/s; r1 = ∞; r2 = 100m; r3 = 200m; g = 10m/s^2
Trọng lực P và phản lực N của mặt cầu đóng vai trò lực hướng tâm
Bài tập 6: Một vật khối lượng 200 g đặt trên mặt bàn quay và cách trục quay 40 cm. Khi bàn quay với tốc độ 72 vòng/min thì vật vẫn nằm yên so với bàn. Tính độ lớn lực ma sát nghỉ của bàn tác dụng lên vật. (ĐS: 4,55 N).
Hướng dẫn giải:
Phân tích bài toán
m = 0,2kg; r = 0,4m; ω = 72vòng/phút = 2,4π (rad/s)
Giải
Fmsn= Fht= mω2r = 4,55N
Bài viết trên đã tổng hợp những kiến thức về lực hướng tâm cũng như những đặc điểm và công thức tính của nó. Hy vọng rằng, thông qua những chia sẻ trên, các em có thể hiểu và áp dụng được để hoàn thành các bài tính toán liên quan. Cảm ơn các em đã đón đọc bài viết.