Hàm số liên tục là một phần kiến thức quan trọng trong Toán Học. Để làm được các bài tập về dạng này bạn cần nắm chắc lý thuyết và các tính chất cơ bản. Dưới đây Wikihoc xin tổng hợp toàn bộ kiến thức và các dạng bài tập giúp bạn học tốt hơn. Hãy cùng theo dõi bài viết này nhé!
Ôn tập lại lý thuyết nền tảng của hàm số
Trước tiên để bắt tay vào làm quen với kiến thức hàm số liên tục. Chúng ta hãy cùng nhau ôn lại kiến thức về hàm số. Vậy hàm số là gì? Tính chất của hàm số cơ bản nào cần nhớ?
Hàm số là gì?
Hiểu một cách đơn giản hàm số chính là một quy tắc được áp dụng trên các số. Nếu ta có một đại lượng y cho trước phụ thuộc vào đại lượng x có giá trị thay đổi. Thì ta luôn xác định được 1 đại lượng y tương ứng. Khi đó đại lượng y được gọi là hàm số của x.
Hay hiểu một cách chi tiết hơn ta có thể định nghĩa khái niệm của hàm số như sau đây:
-
Cho tập D được gọi là tập con khác tập rỗng R. Khi hàm số f xác định trên tập D là một quy tắc với mỗi x đều thuộc D. Khi đó với một số thực y được gọi là giá trị của hàm số f tại điểm x, ta ký kí hiệu như sau y = f(x).
-
Tập D được gọi là tập xác định hay còn gọi là miền xác định. Còn x là đối số hay biến số của hàm số f, ta viết như sau: f: Dx⟶ R ⟼ y = f(x); T = {y = f(x)|x∈D} được gọi là miền giá trị hay tập giá trị của hàm số đó.
Các tính chất hàm số cơ bản cần nhớ
Hàm số có 2 tính chất cơ bản mà bạn cần phải nhớ khi học để ứng dụng vào làm bài tập. Hàm số y = ax + b (a ≠ 0) xác định với mọi x thuộc R.
-
Nếu hệ số a lớn hơn 0 thì hàm số được gọi là đồng biến.
-
Nếu hệ số a nhỏ hơn 0 thì hàm số được gọi là nghịch biến.
Hãy thuộc lòng hai tính chất này để vận dụng vào khi giải các bài tập nhé. Học Toán sẽ trở nên dễ dàng hơn rất nhiều nếu chúng ta nắm chắc phần lý thuyết.
Hàm số liên tục là gì?
Khi đã hiểu về hàm số chúng ta hãy cùng nhau tìm hiểu phần kiến thức sâu hơn đó là hàm số liên tục. Vậy hàm số liên tục khi nào? Và nó liên tục tại những điểm nào?
Trong Toán Học, khi một hàm số được gọi là liên tục tức là nó không có sự thay đổi đột ngột về giá trị. Đây được gọi là những điểm gián đoạn của hàm số. Cụ thể khi đầu vào của hàm số thay đổi ít thì hàm số sẽ có sự chênh lệch đầu ra cũng nhỏ. Khi một hàm số không liên tục thì được gọi là gián đoạn.
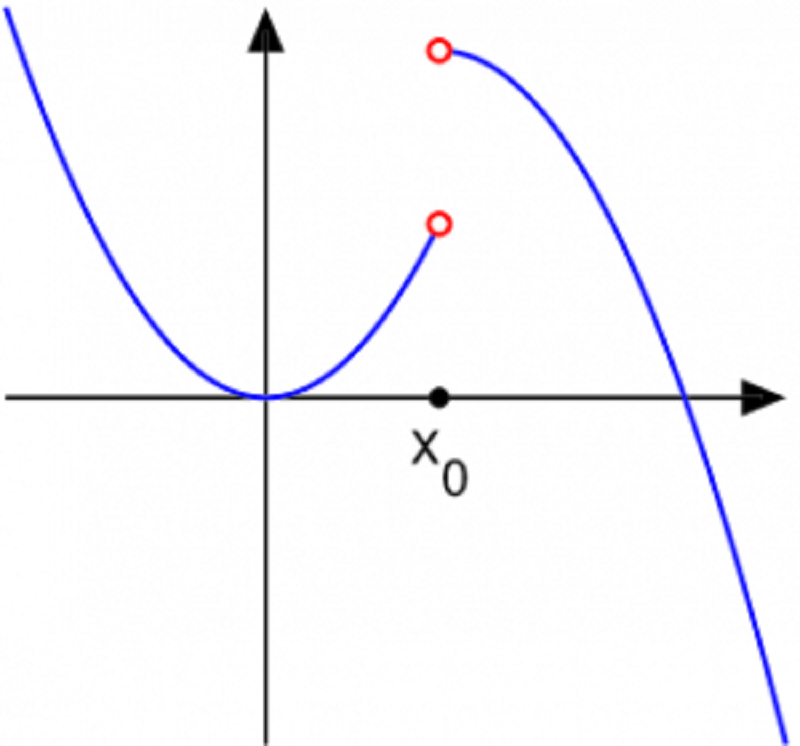
Khi học lên chương trình cao hơn bạn sẽ được tìm hiểu về hàm số liên tục toán cao cấp, hàm số liên tục casio. Đến đây khái niệm về hàm số liên tục lại được hiểu theo một cách trừu tượng khác.
Hàm số liên tục tại một điểm
Cho một hàm số y = f(x) được xác định trên một khoảng (a;b) và x0 thuộc (a;b). Khi đó hàm số f(x) sẽ liên tục tại x0 khi: Lim[x→x0] f(x) = f(x0).Khi hàm số không liên tục tại điểm x0 thì thể gọi là hàm số đang gián đoạn tại x0.
Giả sử các hàm số y = f(x), y = g(x) được coi là liên tục tại điểm x0. Khi đó:
-
Các hàm số y = f(x) + g(x) và y = f(x) – g(x), y = f(x).g(x) sẽ liên tục tại x0.
-
Hàm số y = f(x)/g(x) sẽ liên tục tại x0 nếu g(x0) khác 0.
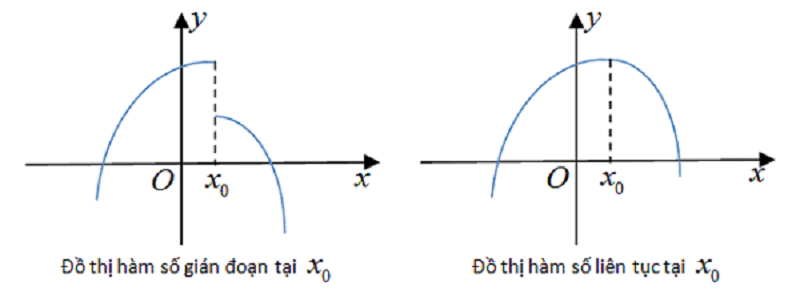
Hàm số liên tục tại một khoảng
- Ta có hàm số y = f(x) sẽ liên tục trên khoảng (a;b) khi nó liên tục tại các điểm nằm thuộc khoảng đó.
- Khi hàm số đã cho liên tục trên khoảng (a;b) thì tương ứng trên khoảng đó, đồ thị của hàm số sẽ là một đường nét liền liên tục và không bị đứt.
Hàm số liên tục tại một đoạn
Hàm số y = f(x) được coi là liên tục trên đoạn [a;b] khi nó liên tục trên mọi điểm tại khoảng (a;b) và khi đó: limx→a + f(x) = f(a), limx→b − f(x) = f(b).
Các định lý cơ bản của hàm số liên tục
Để giúp bạn đọc hiểu sâu hơn về hàm số liên tục. Dưới đây Wikihoc đã tóm lược ngắn gọn những kiến thức về định lý của hàm số liên tục. Hãy cùng theo dõi để làm bài tập tốt hơn nhé!
Định lý 1: Khi tính tổng, tích, thương, hiệu của hai hàm số liên tục với nhau tại một điểm. Thì những hàm số đó sẽ liên tục tại điểm đó ( thương và mẫu tại điểm đó phải khác 0).
Định lý 2:
-
Hàm đa thức liên tục trên R.
-
Hàm lượng giác và phân thức hữu tỉ liên tục trên các khoảng xác định của tập.
-
Các hàm số sơ cấp sẽ luôn liên tục trên những khoảng xác định.
Định lý 3: Nếu hàm số y = f(x) được coi là liên tục trên đoạn [a;b] và f(a).f(b) nhỏ hơn 0 thì sẽ luôn tồn tại ít nhất một điểm c thuộc (a;b) sao cho f(c) = 0.
Các dạng toán về hàm số liên tục thường gặp
Để củng cố thêm kiến thức về hàm số liên tục, dưới đây Wikihoc xin giới thiệu đến bạn một số dạng toán thường gặp về hàm số liên tục.
Dạng 1: Xét tính liên tục của hàm số tại một điểm cụ thể.
Để xét được tính liên tục của một hàm số đã cho trước tại điểm x0 ta thực hiện lần lượt các bước:
- Bước 1: Kiểm tra xem hàm số đã cho có xác định trên một khoảng chứa x0 hay không sau đó hãy tính giá trị tại f(x0).
- Bước 2: Tính limx→x0f(x). Trong nhiều trường hợp ta cần tính limx→x0 + f(x), limx→x0 – f(x).
- Bước 3: So sánh limx→x0f(x) với f(x0) và kết luận.
Dạng 2: Xét tính liên tục, chứng minh hàm số liên tục trên một khoảng đoạn hoặc tập xác định
Để giải được dạng toán này chúng ta hãy cùng nhau xét ví dụ sau đây nhé:
Ví dụ 1: Xét tính liên tục của hàm số: f(x) = (x2+5x)/x khi x khác 0 và khi x = 0, trên R.
Hướng dẫn:
Rõ ràng ta có thể thấy khi x khác 0 thì hàm số đã cho là luôn là hàm phân thức. Và nó hoàn toàn xác định nên nó liên tục trên từng khoảng.
Do đó, lúc này chúng ta chỉ cần xét tính liên tục tại x = 0. Chúng ta có:
Giá trị của hàm số tại x = 0 là f(0) = 5
Giới hạn của hàm số tại x = 0 là limx→0f(x) = limx→0.2 + 5.x = limx→0(x + 5) = 5
Ta thấy limx→0f(x) = f(0) vì vậy mà hàm số đã cho sẽ liên tục tại x = 0
Mẹo nhỏ bạn có thể sử dụng chức năng của máy tính để tính hàm số liên tục bấm máy. Hãy sử dụng phím Solve trên máy để kiểm tra nhanh đáp án của bài toán nhé.
Xem thêm: Lý thuyết về hàm số đồng biến và các dạng bài tập vận dụng thường gặp

Dạng 3: Tìm điều kiện để hàm số liên tục tại một điểm
Để giải được dạng toán này ta sử dụng phương pháp sau. Đầu tiên cần vận dụng điều kiện phương trình có nghiệm và hàm số liên tục:
-
Điều kiện để hàm số liên tục tại x0:
![]()
-
Điều kiện để hàm số đã cho liên tục trên một tập D là f(x) đó là liên tục tại mọi điểm thuộc D.
Phương trình f(x) = 0 phải có ít nhất một nghiệm nếu hàm số y = f(x) liên tục trên D, 2 số a và b đều thuộc D.
Dạng 4: Tìm điều kiện để hàm số liên tục trên một khoảng đoạn hoặc tập xác định
Để giải được dạng này bạn cần áp dụng các định lý 1 và 2 sao cho tìm được tính liên tục của nó trên từng khoảng xác định. Nếu hàm số đã cho được xác định bởi 2 hoặc 3 công thức thì ta sẽ xét tính liên tục tại các điểm đặc biệt đó.
Ví dụ: Tìm a để hàm số liên tục trên tập xác định: f(x) = (2 – 7x + 5×2)/(x – 1) với điều kiện x khác 1 hoặc x = 1
Hướng dẫn cách giải:
-
Đầu tiên xét trường hợp x khác 1 thì hàm số đã cho là phân thức hữu tỉ.
-
Khi x = 1 thay vào hàm số đã cho. Khi đó hàm số f(x) liên tục tại điểm x = 1 khi và chỉ khi m = -4/3.
Dạng 5: Ứng dụng hàm số liên tục chứng minh phương trình có nghiệm
Đầu tiên ta cần áp dụng định lý: Nếu hàm số y = f(x) liên tục trên đoạn [a; b] cho trước và f(a).f(b) nhỏ hơn 0, thì phương trình f(x) = 0 sẽ luôn có ít nhất 1 nghiệm nằm trong khoảng (a; b).
Các bước cụ thể để làm bài chứng minh phương trình có nghiệm như sau:
-
Bước 1: Biến đổi phương trình đã cho cần chứng minh về dạng f(x) = 0.
-
Bước 2: Tiếp theo cần tìm 2 số a và b (a nhỏ hơn b) sao cho f(a).f(b) nhỏ hơn 0
-
Bước 3: Cuối cùng chứng minh hàm số y = f(x) luôn liên tục trên đoạn [a; b] đã cho.
Bài tập về tính chất hàm liên tục để học sinh luyện tập
Ngoài bài tập trong sách giáo khoa toán lớp 11, dưới đây là một số bài tập tham khảo liên quan tới hàm liên tục để các em luyện tập:

Trên đây là những kiến thức tổng hợp về hàm số liên tục. Hy vọng bài viết này sẽ giúp ích cho bạn trong quá trình học tập. Hãy rèn luyện thật kỹ những dạng toán mà Wikihoc đã giới thiệu trong bài viết để học tốt hơn nhé!
