Bội chung nhỏ nhất lớp 6 là một trong những kiến thức toán cơ bản mà các em sẽ được làm quen, học và làm bài tập. Đồng thời, đây cũng là dạng bài tập xuất hiện trong các kỳ thi.
Vậy bội số chung nhỏ nhất là gì? Cách giải toán lớp 6 bội chung và bội chung nhỏ nhất như thế nào? Hãy cùng Wikihoc tìm hiểu chi tiết trong bài viết sau đây nha.
Bội chung và bội chung nhỏ nhất là gì?
Trong chương trình kiến thức toán lớp 6, các em sẽ được làm quen và học bài học về bội chung và bội số chung nhỏ nhất. Cụ thể:
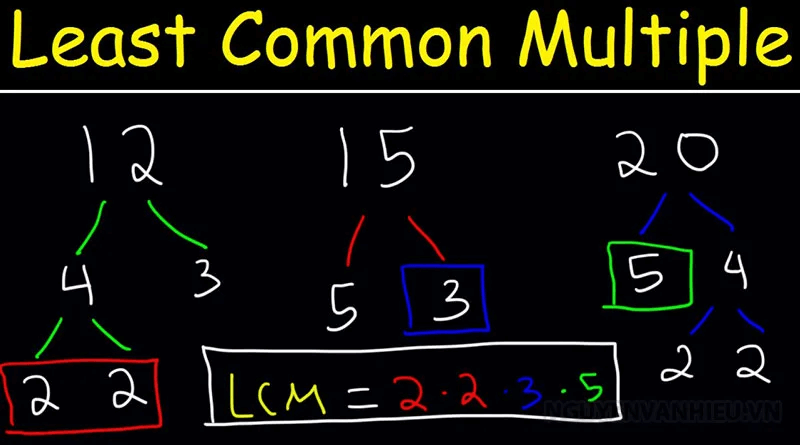
Bội số chung là gì?
Bội số chung được biết đến là tập hợp những số nguyên dương chia hết cho hai hoặc nhiều số nguyên khác nhau. Cụ thể, cho số tự nhiên 1 chia hết cho số tự nhiên b, lúc này ta biết a chính là bội của b.
Bội chung nhỏ nhất là gì?
Bội chung nhỏ nhất (BCNN) của hai số nguyên a và b được biết đến là số nguyên dương nhỏ nhất có thể chia hết được a và b. Nghĩa là, BCNN chính là những số có thể chia được hết cho a và b mà không có dư. Trường hợp, nếu a hoặc b bằng 0 sẽ không tồn tại BCNN.
Ký hiệu
Bội số chung nhỏ nhất của hai số a và b sẽ được ký hiệu như sau: [a, b], BCNN (a, b).
Ví dụ: BCNN (5, 10, 20) = BCNN (5, 10), BCNN (10, 2) = 20;
Khi nào cần tìm BCNN của hai số?
Trước khi tìm hiểu cách tìm bội chung nhỏ nhất lớp 6, đòi hỏi các em cần phải biết được khi nào nên tìm BCNN. Cụ thể, BCNN của hai số là dạng kiến thức được ứng dụng trong rất nhiều bài tập khác nhau từ dạng số nguyên, dạng lũy thừa, dạng phân số,… để có thể rút gọn số nhanh chóng.
Đặc biệt, ở dạng toán rút gọn phân số thì việc tìm được BCNN giúp ích rất nhiều để có thể đưa phân số đó về dạng tối giản nhất để thực hiện phép tính nhanh chóng hơn. Còn các bài toán về số nguyên cũng có thể tìm BCNN để tính toán dễ dàng hơn.

Cách tìm bội chung nhỏ nhất lớp 6 như thế nào?
Trong toán lớp 6 bội chung và bội chung nhỏ nhất, để tìm được BCNN của hai hoặc nhiều số lớn hơn 1 thì mọi người chỉ cần áp dụng theo 3 bước sau:
-
Bước 1: Tiến hành tính toán mỗi số ra thừa số nguyên tố.
-
Bước 2: Lựa chọn ra những thừa số nguyên tố chung và riêng.
-
Bước 3: Bắt đầu lập tích các thừa số đã chọn, sau đó mỗi thừa số lấy với số mũ lớn nhất của nó. Lúc này, tích đó chính là BCNN đang tìm.
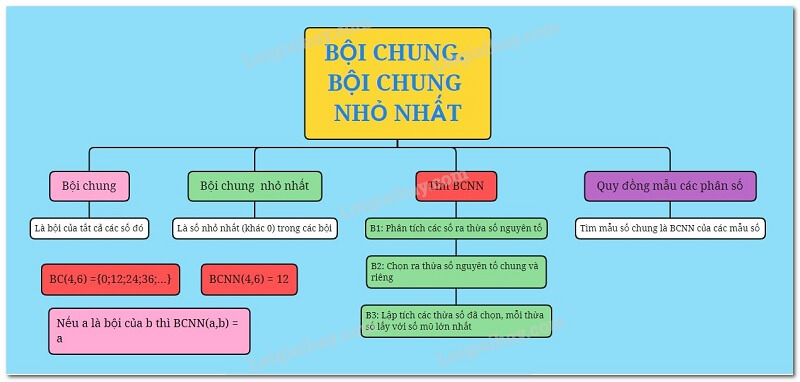
Chú ý:
- Nếu những số đã cho từng đôi một nguyên tố cùng nhau, lúc này BCNN cần tìm chính là tích của những số đó.
- Với những số đã cho, nếu số lớn nhất chính là bội số chung của những số còn lại thì BCNN cần tìm chính là số lớn nhất đó.
Ví dụ:
BCNN (5, 7) = 5.7 = 35. Bởi vì 5 và 7 cùng là số nguyên tố, lúc này BCNN chính là tích của 2 số đó là 35.
BCNN (8, 12, 96) = 96. Bởi vì 96 chia hết được 8 và 12, lúc này BCNN cần tìm của 3 số chính là số lớn nhất đó là 96.
Tìm giá trị của BCNN (8,9,21).
Đầu tiên, mọi người cần phân tích những số nguyên đã cho thành dạng lũy thừa các số nguyên tố. Với mỗi số tìm được, bạn sẽ tính lũy thừa cao nhất, tích của chúng chính là BCNN đang tìm. Cụ thể là 2, 3, 5 và 7, bậc cao nhất lúc này lần lượt là 23, 32, 30, và 71. Lúc này, ta tìm được BCNN (8, 9, 21) chính à 8.9.1.7 = 504.
Các dạng bài tập bội chung và bội chung nhỏ nhất lớp 6
Đối với toán bội chung và bội chung nhỏ nhất lớp 6 sẽ có nhiều dạng bài tập khác nhau để các em chinh phục, cụ thể:

Dạng 1: Dạng bài tìm BCNN của một số cho trước
Với dạng bài tập này sẽ yêu cầu học sinh tìm bội số chung nhỏ nhất của 2 hoặc nhiều số. Phương pháp giải cũng khá đơn giản, các em chỉ cần áp dụng quy trình cách tìm bội chung nhỏ nhất lớp 6 trên sẽ tìm được đáp án chính xác.
Ví dụ: Tìm BCNN của 30 và 150
Giải: BCNN (30, 150) = 150 vì 150 chia hết cho 30;
Dạng 2: Bài toán là tìm BCNN của một số đã cho
Với dạng bài tập tìm bội chung nhỏ nhất này, các em cần phải phân tích đề bài, rồi bắt đầu suy luận về việc tìm BCNN của 2 hay nhiều số chính xác.
Dạng này các bạn phải phân tích đề bài, suy luận để đưa về việc tìm BCNN của hai hay nhiều số.
Ví dụ: Tìm số tự nhiên a nhỏ nhất khác 0, biết rằng a chia hết cho 15 và 18.
Giải:
a chia hết cho 15 và 18 nên a được xem là bội chung của 15 và 18 .
a lại là số nhỏ nhất khác 0 nên ta có thể suy luận ra được a là BCNN (15, 18) = 90.
Dạng 3: Tìm BCNN của hai hoặc nhiều số thỏa mãn các điều kiện nhất định
Với dạng bài tập này, các em cũng cần phải phân tích đề bài, sau đó sẽ suy luận đưa về dạng tìm BCNN nhỏ hoặc nhiều số cho trước. Đảm bảo:
-
Tìm BCNN của các số đó;
-
Tìm các bội của BCNN này ;
-
Chọn trong số đó các bội thỏa mãn điều kiện đã cho.
Ví dụ: Học sinh lớp 6A khi xếp hàng 2, 3, 4 và 8 đều đủ hàng. Biết rằng, số học sinh lớp 6A khoảng từ 35 – 60 em. Tính tổng số học sinh lớp 6A là bao nhiêu?
Giải:
Dựa vào đề bài ta biết được số học sinh lớp 6A phải chia hết cho 2, 3, 4 và 8. Lúc này ta phải tìm được con số là bội chung của các số đó. Cụ thể:
BCNN(2, 3, 4, 8) = 24 ; Suy ra, B(24) = {0 ; 24 ; 48 ; 72 ; 96 ; …}
Bên cạnh đó, đề bài còn đưa ra số học sinh lớp 6A nằm trong khoảng 35 – 60, nên với các số thuộc B(24) trên chỉ có 48 là thỏa mãn điều kiện. Lúc này, tổng số học sinh lớp 6A tương ứng là 48 em.
Các bài tập bội chung nhỏ nhất lớp 6 để bé tự luyện
Dưới đây là một số bài tập toán lớp 6 bội chung và bội chung nhỏ nhất để các bé cùng nhau luyện tập hiệu quả.

Kết luận
Trên đây là những thông tin giúp mọi người hiểu rõ hơn về kiến thức bội chung và bội chung nhỏ nhất lớp 6. Đây là một dạng kiến thức quan trọng, thường sẽ xuất hiện nhiều trong các đề thi, nên các em cần ôn luyện, áp dụng cách tìm mà Wikihoc chia sẻ trên để có thể chinh phục dạng toàn này hiệu quả nhé.
