Công thức nguyên hàm là một phần kiến thức vô cùng quan trọng trong chương trình giải tích của lớp 12. Đặc biệt hơn, đây còn là nội dung thường được đưa vào bộ đề thi THPT Quốc Gia nhiều năm gần đây.
Tuy nhiên, không phải bạn học sinh nào cũng có thể nắm vững và ghi nhớ một cách đầy đủ các công thức. Bởi vậy, trong bài viết dưới đây, Wikihoc sẽ tổng hợp bảng nguyên hàm lớp 12 thường gặp và chi tiết nhất để giúp bạn chinh phục được mọi bài toán cơ bản và nâng cao bạn nhé!
Khái niệm nguyên hàm là gì?
Để hiểu được bản chất của một công thức thì đầu tiên chúng ta cần thuộc và biết rõ về định nghĩa của công thức đó. Theo đó, nguyên hàm của một hàm số thực f cho trước là một hàm F khi đạo hàm có cho kết quả bằng chính f, cụ thể, F′ = f.
Nghĩa là với một hàm số f(x) xác định tại một khoảng K cho trước. F(x) được gọi là nguyên hàm của f(x) trên K khi F’(x)=f(x) với mọi x thuộc K
Từ những tìm hiểu để biết nguyên hàm là gì và khái niệm đưa ra như trên, các nhà toán học đã xây dựng nên các công thức nguyên hàm để áp dụng trong giải các bài toán bao gồm cả cơ bản và nâng cao. Dưới đây, Wikihoc sẽ tổng hợp chi tiết bảng công thức nguyên hàm toán 12 mà học sinh cần phải nắm chắc.
Tổng hợp chi tiết các công thức nguyên hàm thường gặp
Công thức nguyên hàm cơ bản
Trong phần công thức nguyên hàm toán 12 cơ bản, Wikihoc sẽ chia bảng ra làm hai mục bao gồm nguyên hàm của các hàm số sơ cấp thường gặp và nguyên hàm của các hàm số hợp. Khi học sinh hiểu kỹ được định nghĩa toán đã nói bên trên thì các em sẽ dễ dàng ghi nhớ được các công thức nguyên hàm cơ bản này. Chúng mình hãy cùng xem và học thuộc bảng nguyên hàm 12 dưới đây nhé!
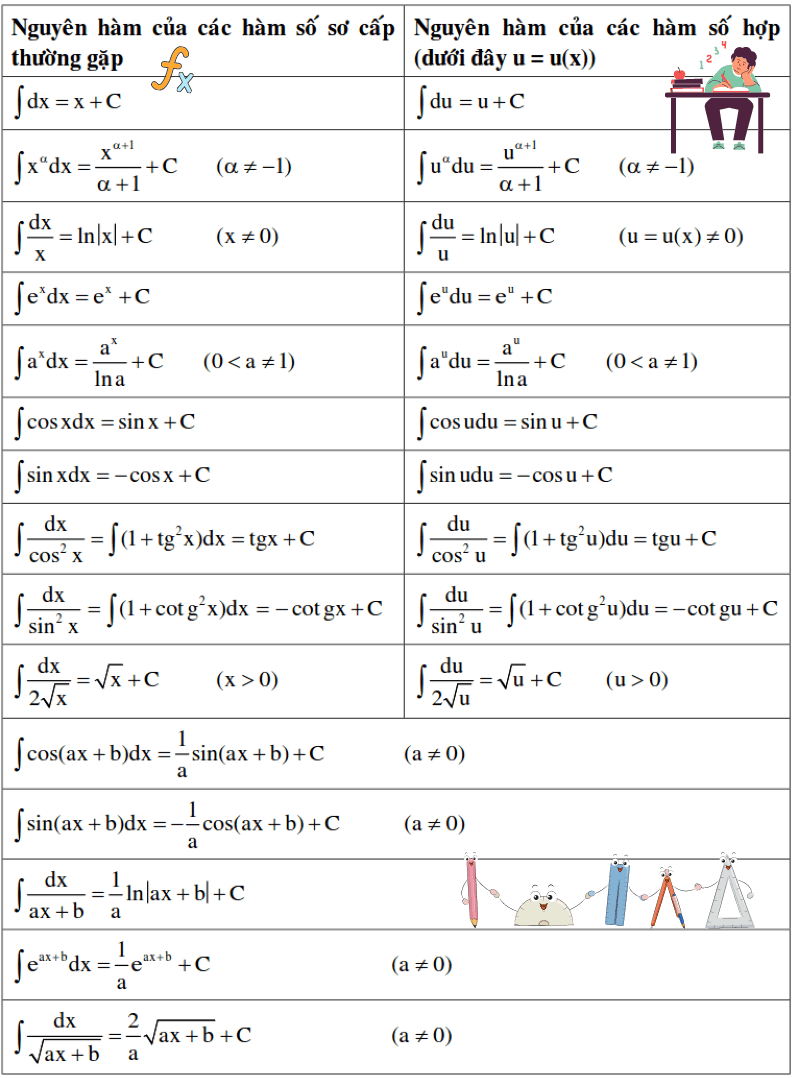
Công thức nguyên hàm nâng cao
Đây là các công thức toán nguyên hàm đòi hỏi ở mức độ cao hơn đối với các bạn học sinh. Những nguyên hàm này thường phức tạp và khó để ghi nhớ. Do đó, học sinh cần nắm chắc kiến thức cơ bản về định nghĩa toán, các hàm cơ bản trước rồi mới chuyển sang học toán nguyên hàm nâng cao.
Đồng thời, chúng ta cũng nên tránh tình trạng học vẹt mà thay vào đó hãy sử dụng phương pháp phân tích logic để hiểu rõ bản chất của từng công thức toán. Như vậy, học sinh sẽ dần vững hơn khi gặp các bài toán khó và linh hoạt trong việc vận dụng các công thức nguyên hàm. Dưới đây là bảng tổng hợp các nguyên hàm nâng cao thường gặp mà các bạn học sinh nên biết.

Một số ví dụ thường gặp có áp dụng công thức nguyên hàm
Để giúp các bạn học sinh hiểu hơn về các công thức nguyên hàm được tổng hợp bên trên, Wikihoc sẽ cung cấp một vài dạng bài tập chính thường gặp và các ví dụ mẫu với lời giải chi tiết có sử dụng phương pháp tính nguyên hàm như sau.
Các dạng bài tập tính nguyên hàm
Lưu ý, để đơn giản hơn trong quá trình giải toán và tránh những nhầm lẫn không đáng có khi áp dụng công thức tính nguyên hàm, các bạn học sinh nên đặt các hàm số mà đề bài đã cho về các hàm u hoặc v. Các dạng thường gặp bao gồm:
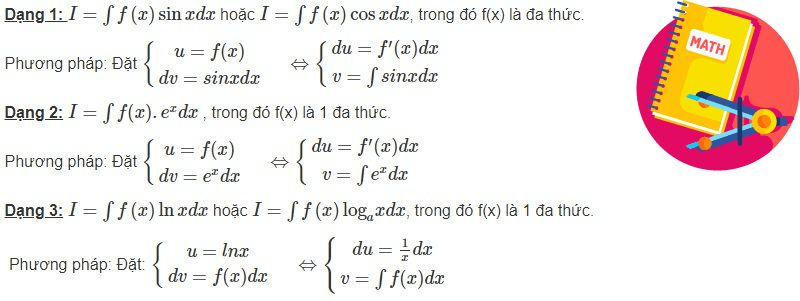
Ví dụ áp dụng công thức nguyên hàm và lời giải chi tiết
Từ 3 dạng chính thường gặp bên trên, các nhà làm giáo dục đã phát triển thành nhiều bài toán từ cơ bản đến nâng cao và đòi hỏi học sinh phải vận dụng công thức nguyên hàm một cách khéo léo nhất. Sau đây, Wikihoc xin gửi tới những bài mẫu có lời giải đầy đủ và chi tiết mà bạn có thể tham khảo.
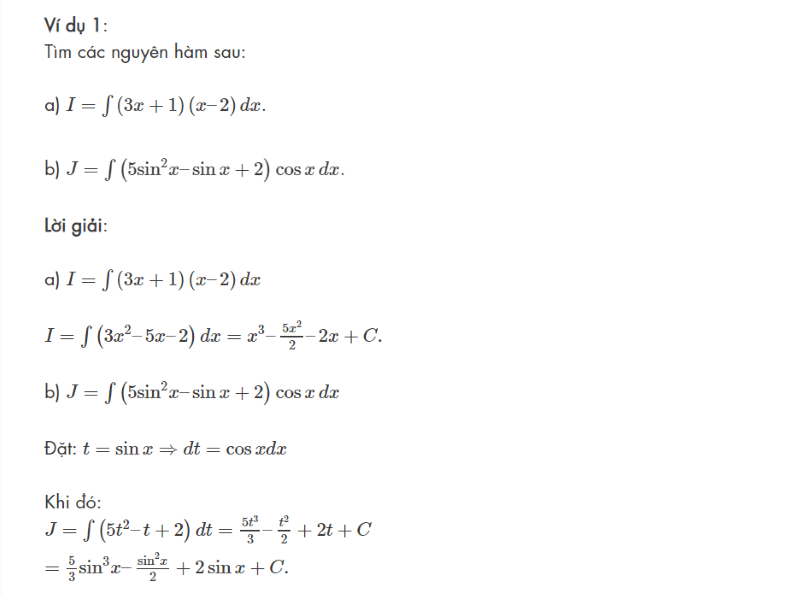

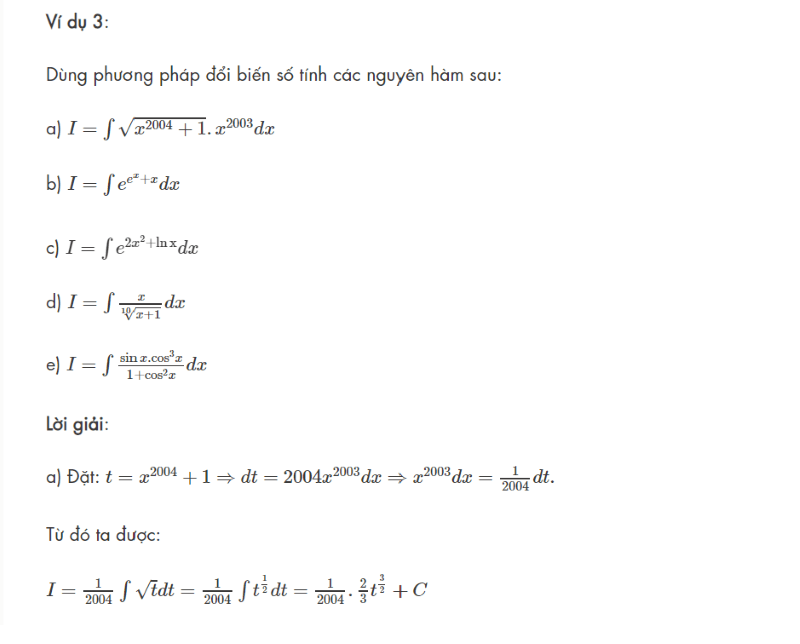
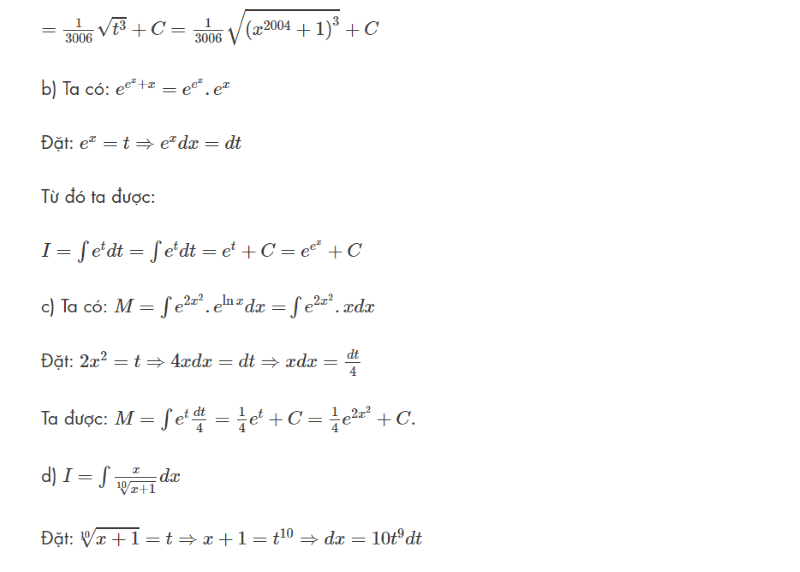
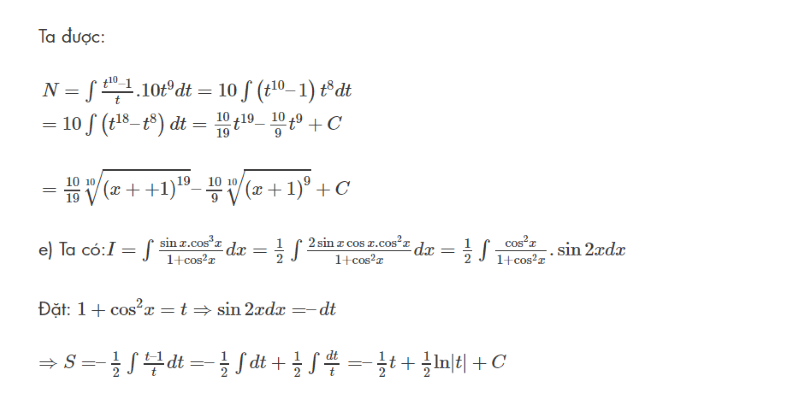
Một mẹo nhỏ mà Wikihoc mách đến bạn là hãy xem kỹ những cách làm trên. Và sau đó tự giải lại bài toán bằng nhiều phương pháp khác nhau theo cách hiểu của bản thân.
Xem thêm: Nguyên hàm từng phần là gì? Công thức tính nguyên hàm từng phần cơ bản và nâng cao đầy đủ nhất
Cách ứng dụng công thức nguyên hàm trong thực tế
Công thức nguyên hàm được ứng dụng nhiều vào cuộc sống để tính vận tốc, gia tốc và quãng đường chuyển động của vật hoặc người. Từ đây, bạn đọc có thể thấy tính thực tế và ý nghĩa cao của nguyên hàm. Dưới đây là một vài ví dụ về công thức nguyên hàm được ứng dụng cũng như đưa vào các bài toán trong chương trình toán 12.


Những lưu ý khi học và ghi nhớ công thức nguyên hàm
Khi nhìn bảng tổng hợp công thức nguyên hàm ở trên, chắc chắn nhiều bạn học sinh sẽ cảm thấy ngao ngán và tự hỏi có cách nào để giúp việc ghi nhớ nguyên hàm trở nên dễ dàng hơn không. Thật ra, không có bất kỳ phương pháp cố định và cụ thể nào, mà tất cả đều dựa vào ý chí cũng như sự quyết tâm của mỗi người.
Do đó, những lưu ý sau của Wikihoc sẽ chỉ là một vài bí quyết để góp phần nhỏ trong hành trình học nguyên hàm lớp 12 của các bạn. Hãy cùng xem đó là gì nhé!
-
Học chắc kiến thức cơ bản về khái niệm, tính chất của nguyên hàm.
-
Hiểu rõ nguyên nhân và hệ quả của từng công thức.
-
Vận dụng công thức nguyên hàm để giải nhiều dạng bài tập khác nhau.
-
Lắng nghe thầy cô giáo giảng bài trên lớp và học nhóm cùng bạn bè.
-
Tự tìm ra những cách giải hay và học bổ sung những phần chưa hiểu tại nhà.
Vậy là thông qua bài viết trên, Wikihoc đã gửi tới bạn đọc những công thức nguyên hàm cần biết bao gồm cơ bản và nâng cao. Bên cạnh đó là những mẹo học và lưu ý quan trọng cần biết. Hy vọng các bạn học sinh sẽ áp dụng thật thành thạo các công thức trong quá trình tính nguyên hàm và không còn cảm giác lo lắng hay sợ hãi mỗi khi học toán nữa nhé!
