Hình tam giác là gì? Tất tần tật kiến thức chi tiết đầy đủ nhất

Trong các loại hình học, hình tam giác là một hình khá đặc biệt khi bản thân chúng có nhiều hình đi kèm như tam giác cân, tam giác đều,…nên lượng kiến thức học sẽ nhiều hơn. Để giúp bé học hiểu và áp dụng tốt kiến thức này, hãy cùng Wikihoc tìm hiểu rõ hơn ngay bài viết sau đây.

Mục Lục Bài Viết

Hình tam giác là gì?

Trong các loại hình học cơ bản, Tam giác là một hình học phẳng cơ bản có 3 đỉnh không thẳng hàng với nhau. 3 điểm này được hình thành từ 3 đoạn thẳng nối với nhau. Đồng thời đây là hình đa giác với số cạnh ít nhất là 3.

Ngoài ra, tam giác luôn là hình đa giác đơn và thuộc vào đa giác lồi. Nghĩa là các góc của hình tam giác luôn nhỏ hơn 180 °,còn các góc của hình gọi là góc trong, góc ngoài sẽ bằng tổng góc trong không kề bù với nó. Suy ra, mỗi tam giác chỉ có 3 góc trong và 6 góc ngoài.

Tính chất hình tam giác

Tổng số đo các góc trong của 1 hình tam giác bằng 180°.
Độ dài mỗi cạnh sẽ lớn hơn hiệu độ dài 2 cạnh còn lại, nhỏ hơn tổng độ dài của chúng.
Trong 1 hình tam giác, cạnh đối diện với góc lớn hơn chính là cạnh lớn nhất. Ngược lại, góc đối diện cạnh lớn hơn chính là góc lớn hơn.
3 đường cao của hình tam giác sẽ cắt nhau tại 1 điểm gọi là trực tâm của tam giác.
3 đường trung tuyến hình tam giác cắt nhau tại 1 điểm gọi là trọng tâm. Hay 3 đường trung tuyến của hình đồng quy tại 1 điểm, khoảng cách từ trọng tâm đến 3 đỉnh tam giác sẽ bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó. Đồng thời, đường trung tuyến tam giác sẽ chia hình làm 2 phần có diện tích bằng nhau.
3 đường trung trực của tam giác cắt nhau tại một điểm là tâm đường tròn ngoại tiếp của tam giác.
3 đường phân giác trong của hình tam giác cắt nhau tại một điểm là tâm đường tròn nội tiếp của tam giác.
Trong hình tam giác, đường phân giác của một góc chia cạnh đối diện thành 2 đoạn thẳng tỷ lệ với 2 cạnh kề 2 đoạn thẳng đó.

Các đường đặc biệt của hình tam giác cần nắm rõ

Khi tìm hiểu kiến thức về hình tam giác, học sinh cũng cần nắm rõ các đường đặc biệt thuộc hình này như:

Đường trung tuyến: Đường thẳng nối một đỉnh với trung điểm của cạnh đối diện nó. Nên trong 1 hình tam giác sẽ có 3 đường trung tuyền và chúng giao nhau tại 1 điểm.

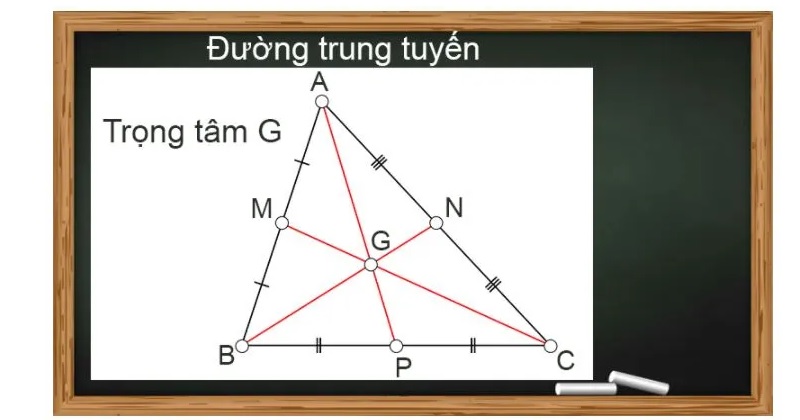
Đường cao: Đường thẳng từ đỉnh hạ vuông góc xuống cạnh đối diện. Tương ứng trong 1 hình tam giác có 3 đường cao và chúng giao nhau tại 1 điểm.

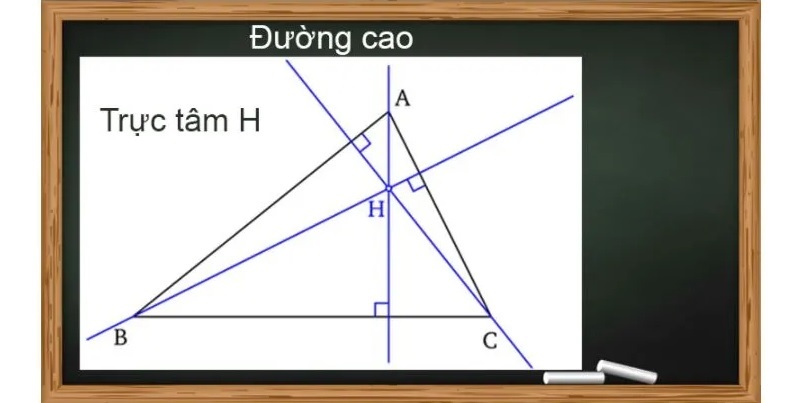
Đường trung trực: Đường thẳng vuông góc với đoạn thẳng tại trung điểm của chính đoạn thẳng đó. Trong một hình tam giác sẽ có 3 đường trung trực, giao nhau tại 1 điểm.

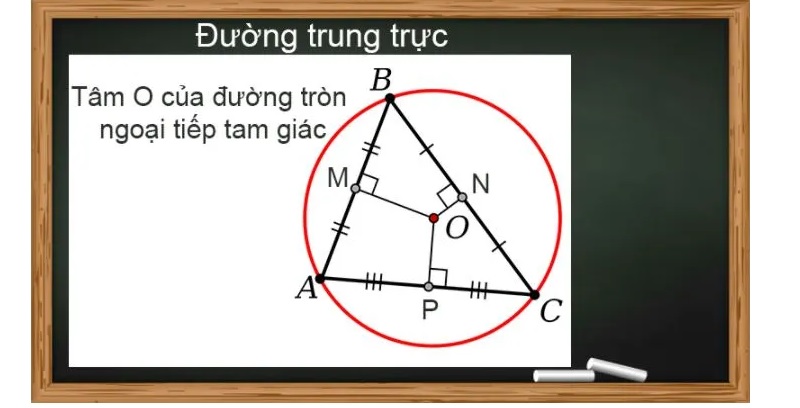
Đường trung bình: Đường thẳng nối trung điểm 2 cạnh tam giác.

Tham khảo thêm: Công thức tính chu vi hình tam giác Chu vi tam giác cân, đều, vuông

Đường tròn ngoại tiếp tam giác: Đường tròn đi qua 3 đỉnh của giác giác.

Đường tròn nội tiếp tam giác: Đường tròn tiếp xúc với 3 cạnh của tam giác.

Sự bằng nhau giữa các tam giác như thế nào?

Hai hình tam giác bằng nhau chính là 2 tam giác có các cạnh và góc tương ứng bằng nhau. Dưới đây là những trường hợp bằng nhau của các hình tam giác:

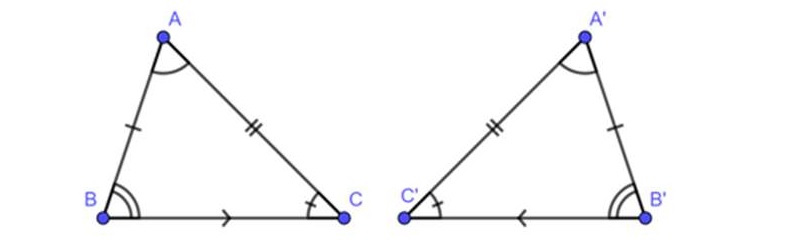
Cạnh – cạnh – cạnh (c.c.c): Nếu 3 cạnh tam giác này bằng 3 cạnh tam giác kia thì đó là 2 hình tam giác bằng nhau.
Cạnh – góc – cạnh (g.c.g): Nếu 2 cạnh và góc xen giữa của tam giác này bằng 2 cạnh và góc xen giữa tam giác kia thì 2 hình tam giác đó bằng nhau.
Góc – cạnh – góc (g.c.g): Nếu hình tam giác có 1 cạnh và 2 góc kề bằng với 1 cạnh và 2 góc kề của tam giác kia thì 2 tam giác đó bằng nhau.
Hai cạnh góc vuông: Nếu tam giác có 2 cạnh góc vuông bằng với 2 cạnh góc vuông của tam giác kia thì đó là 2 tam giác bằng nhau. (cạnh – góc – cạnh)
Cạnh góc vuông và góc nhọn kề cạnh đó: Hình tam giác có cạnh góc vuông cùng 1 góc nhọn kề cạnh đó bằng 1 cạnh góc vuông và 1 góc kề cạnh đó của tam giác khác thì đó là 2 tam giác bằng nhau. (góc – cạnh – góc).
Cạnh huyền – góc nhọn: Nếu cạnh huyền cùng 1 góc nhọn tam giác vuông này bằng cạnh huyền và góc nhọn tam giác vuông kia thì đó là 2 tam giác vuông bằng nhau.
Cạnh huyền – cạnh góc vuông: Nếu tam giác vuông này có cạnh huyền và cạnh góc vuông cũng bằng với cạnh huyền và cạnh góc vuông của tam giác vuông kia, đó là 2 tam giác vuông bằng nhau.

Sự đồng dạng giữa các tam giác

Trong hình học, 2 tam giác được xem là đồng dạng với nhau khi chúng thỏa mãn những trường hợp sau:

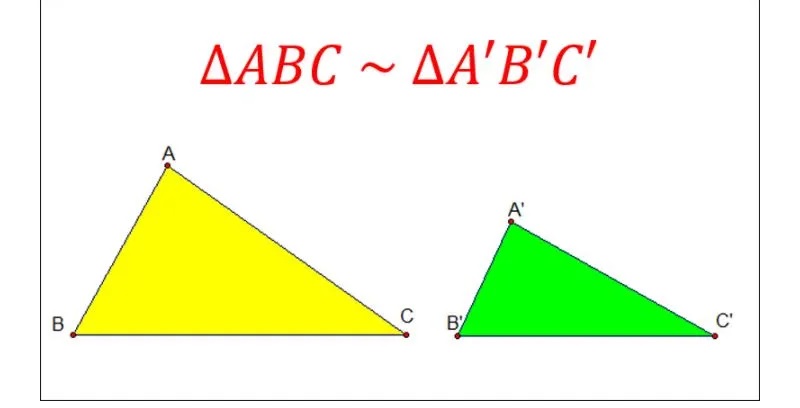
Trường hợp 1: Hai hình tam giác có 3 cặp cạnh tương ứng tỷ lệ với nhau thì đồng dạng (c.c.c)
Trường hợp 2: Hai hình tam giác có cặp góc bằng nhau thì đồng dạng (g.g)
Trường hợp 3: Hai hình tam giác có 2 cặp cạnh tương đồng với tỷ lệ góc xen giữa hai cặp cạnh đó bằng nhau cũng sẽ đồng dạng (c.g.c).
Trường hợp 4: Hai hình tam giác bằng nhau sẽ đồng dạng.

Xem thêm:

Công thức tính diện tích hình vuông là gì? Bài tập và bí quyết thực hành hiệu quả
Nguyên hàm từng phần là gì? Công thức tính nguyên hàm từng phần cơ bản và nâng cao đầy đủ nhất
Cách tính bán kính hình tròn đơn giản và bài tập tự luyện hiệu quả

Phân loại các hình tam giác thường gặp

Tam giác là một trong những hình học có nhiều thể loại khác nhau. Dưới đây là phân loại chi tiết một số hình tam giác thường gặp như:

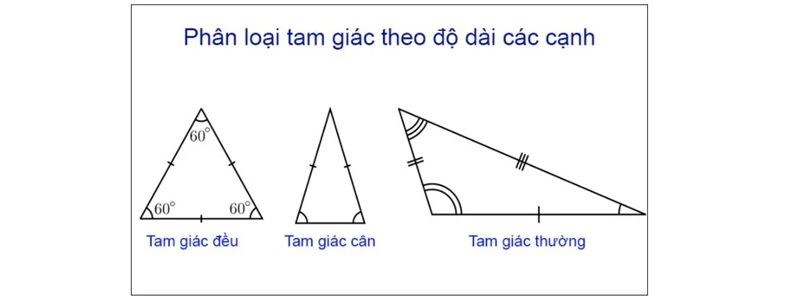
Phân loại theo độ dài cạnh

Tam giác thường: Có độ dài các cạnh và góc khác nhau (bao gồm cả trường hợp đặc biệt của tam giác).
Tam giác cân: Có 2 cạnh bằng nhau
Tam giác đều: cả 3 cạnh bằng nhau

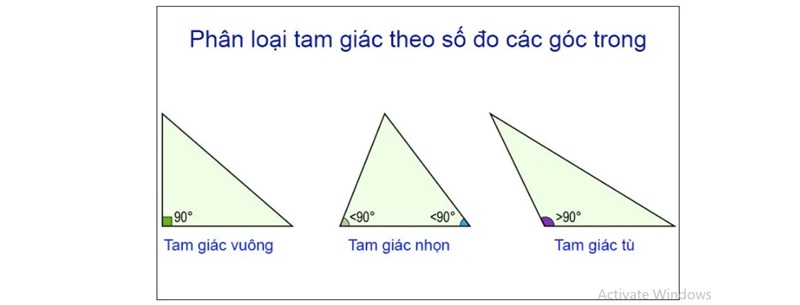
Theo số đo các góc trong

Tam giác vuông: Có 1 góc bằng 90 °
Tam giác tù: Có 1 góc nhỏ hơn 90 ° hay có 6 góc ngoài lớn hơn 90 °
Tam giác vuông cân: Vừa là tam giác vuông vừa là tam giác cân. Nghĩa là có 1 góc vuông 90 ° cùng 2 góc nhọn bằng 45 °.

Các công thức liên quan của tam giác

Khi học toán về hình tam giác, các em cần phải nắm rõ những công thức sau để làm bài tập và ứng dụng trong thực tế chính xác:

Chu vi tam giác: P = a + b + c.

Trong đó:

P: Chu vi tam giác
a, b, c: độ dài các cạnh tam giác

Diện tích tam giác: S = ( a x h) /2

Trong đó:

S: Diện tích tam giác
a: Chiều dài đáy
h: Chiều cao tam giác

Lưu ý: Tùy vào từng hình tam giác sẽ có công thức tính chu vi và diện tích khác nhau. Tìm hiểu rõ hơn tại bài “diện tích tam giác” và “chu vi tam giác” mà Wikihoc đã chia sẻ.

Tham khảo thêm:

Những định lý được áp dụng trong hình tam giác

Khi học toán, các em học sinh cần ghi nhớ các định lý trong tam giác như sau:

Định lý Pythagoras: Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương của hai cạnh góc vuông. Được viết bởi hệ thức: a2 = b2 + c2

Định lý Apollonius: Với một tam giác ABC, và AD là đường trung tuyến ta có hệ thức: AB2 + AC2 = 2(AD2 +BD2)

Định lý Stewart: Gọi a, b, và c là độ dài các cạnh của một hình tam giác. Gọi d là độ dài của đoạn thẳng nối từ một đỉnh của tam giác với điểm nằm trên cạnh (ở đây là cạnh có độ dài là a) đối diện với đỉnh đó. Đoạn thẳng này chia cạnh a thành hai đoạn có độ dài m và n, định lý Stewart sẽ có hệ thức: b2m + c2n = a(d2 +mn).

Định lý Thales: Có một đường thẳng cắt hai cạnh của một hình tam giác và song song với cạnh còn lại thì sẽ xuất hiện những cặp đoạn thẳng tỉ lệ trên hai cạnh được cắt đó.

Các dạng toán thường gặp khi học toán hình tam giác

Đối với học sinh cấp tiểu học, thường các bài tập liên quan tới hình tam giác chưa đòi hỏi quá nhiều kiến thức nâng cao. Đa phần các em sẽ được thử sức với những dạng toán sau đây:

Dạng 1: Tính chu vi hình tam giác

Đây được xem là một trong những dạng bài tập toán cơ bản của hình tam giác. Ở đây thường sẽ yêu cầu học sinh tính chu vi tam giác khi cho biết dữ kiện về các cạnh.

Để giải, học sinh cần biết được đó là hình tam giác gì rồi tiến hành áp dụng đúng công thức tính chu vi của tam giác đó để tìm đáp án chính xác.

Ví dụ: Tính chu vi tam giác vuông với độ dài CA = 5cm, CB = 9cm và AB = 15cm.

Dựa vào công thức tính chúng ta có cách tính P = 5 + 9 + 15 = 29cm.

Dạng 2: Tính diện tích hình tam giác

Cũng tương tự như bài tập trên, ở đây các em cũng sẽ phải xác định rõ đó là hình tam giác gì? cùng với dữ kiện mà đề bài cho để tiến hành áp dụng công thức và tìm ra đáp án chính xác.

Ví dụ: Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 24dm.

Giải: Chiều cao 24dm = 2,4m

Diện tích tam giác là: S = (5×2.4)/2 = 6m2

Xem thêm: Diện tích hình tam giác và bí quyết giúp em học đơn giản dễ hiểu hơn

Dạng 3: Nhận biết các hình tam giác

Với bài tập này, thường đề bài sẽ cho một vài hình tam giác khác nhau, yêu cầu học sinh phân biệt đó là tam giác gì?

Để giải, đòi hỏi các em phải nắm rõ đặc điểm từng hình tam giác cân, vuông, đều… để có thể giải bài tập chính xác.

Ví dụ: Các hình bên dưới thuộc hình tam giác gì?

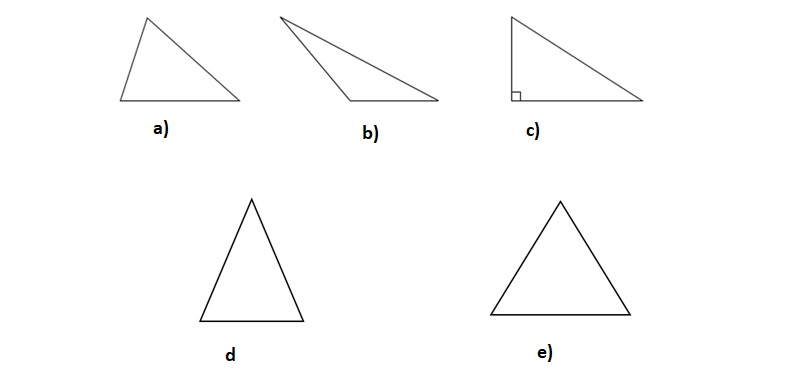
Câu trả lời:

Hình a: tam giác thường, với 3 góc nhọn
Hình b: Tam giác thường với 2 góc tù, 1 góc nhọn
Hình c: Tam giác vuông, vì có 1 góc vuông
Hình d: Tam giác cân, vì 2 cạnh bên bằng nhau
Hình e: Tam giác đều, vì 3 cạnh bằng nhau.

Dạng 4: Công thức, định nghĩa

Ở bài tập này thường sẽ thuộc phần trắc nghiệm khi chọn đáp án đúng khi nói về đặc điểm, tính chất nào đó liên quan tới hình tam giác. Nên đòi hỏi học sinh phải nắm vững phần lý thuyết mới trả lời chính xác.

Ví dụ:

Cho nhận xét sau: “……….. là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng 60 °. Điền từ thích hợp vào chỗ trống.

A. Hình vuông

B. Hình lục giác đều

C. Hình tam giác đều

D. Cả A, B và C đều sai.

Đáp án: C. Vì tam giác đều là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng 60 °.

Bài tập toán tam giác để bé luyện tập

Dưới đây là tổng hợp một số bài tập về hình tam giác để bé tham khảo và cùng luyện tập:

Tham khảo thêm:

Bí quyết giúp bé học, ghi nhớ kiến thức hình tam giác hiệu quả

Đối với kiến thức về hình tam giác khá nhiều, nên nhiều bé sẽ cảm thấy hơi khó. Vậy nên, để giúp quá trình học, lĩnh hội kiến thức này của bé hiệu quả., bố mẹ có thể áp dụng một số bí quyết sau đây:

Nâng cao năng lực học toán toàn diện cùng Wikihoc Math

Wikihoc Math là ứng dụng toán tiếng Anh hàng đầu Việt Nam dành cho trẻ mầm non và tiểu học. Nội dung bài học mà ứng dụng cung cấp giúp các bé dễ dàng tiếp cận với chương trình toán học Mỹ sinh động và toàn diện hơn.

Để qua đó giúp trẻ vừa được học tập, trải nghiệm, khám phá, ôn luyện kiến thức nhuần nhuyễn và hứng thú hơn thay vì chỉ học trên sách vở.

Cụ thể, hệ thống chương trình học tại Wikihoc Math sẽ chia ra thành 4 cấp độ khác nhau từ cơ bản đến nâng cao, chia thành 400+ bài học thú vị, 10.000+ hoạt động tương tác cùng 60+ chủ đề Toán học bám sát theo Chương trình GDPT Mới cho trẻ Mầm non và Tiểu học.

Thậm chí có nhiều chủ đề toán theo tiêu chuẩn Mỹ chưa có trong chương trình của Việt Nam (ví dụ: các chủ đề liên quan tới quy luật, biểu đồ thống kê và hình khối) để giúp bé làm quen và học tập hiệu quả hơn)

Tất cả bài học trong Wikihoc Math đều được thiết kế chặt chẽ để cá nhân hóa phù hợp với từng độ tuổi, cùng với hoạt động ôn luyện, học tập và lĩnh hội kiến thức hiệu quả nhất.

Ngoài ra, điểm đặc biệt khi cho bé học toán cùng Wikihoc Math chính là học hoàn toàn bằng tiếng Anh Mỹ. Kết hợp cùng giọng đọc chuẩn Mỹ, hình ảnh miêu tả sinh động sẽ giúp các con vừa được học toán, vừa học tiếng Anh một cách tự nhiên nhất.

Đồng thời, các bài học tại Wikihoc Math đều được thiết kế dưới dạng các video trò chơi tương tác có nội dung vui nhộn. Để qua đó bé sẽ có sự hứng thú hơn khi học tập, tiếp thu kiến thức mà không hề nhàm chán.

Hứa hẹn, với việc học toán với Wikihoc Math cùng bé sẽ là những giây phút thoải mái, hứng thú mà vẫn đảm bảo hiệu quả học tập của con tốt nhất.

Đảm bảo bé nắm vững kiến thức cơ bản về hình tam giác

Với chuyên đề “hình tam giác” không chỉ được học ở cấp 1, mà xuyên suốt chương trình học các cấp và thậm chí ngoài thực tế vẫn sẽ tiếp tục ứng dụng. Nhưng kiến thức cơ bản trên là điều quan trọng nhất để làm tiền đề cho các kiến thức nâng cao hơn.

Chính vì vậy, bố mẹ hãy đảm bảo các bé đã nắm vững được các kiến thức cơ bản liên quan như các loại hình tam giác, đặc điểm của từng hình, các tính chất, công thức,…

Để làm được điều này, bạn nên kiểm tra kiến thức của con thường xuyên để xem bé nhớ bài học đến đâu, còn yếu phần nào và tiến hành hướng dẫn, củng cố kiến thức cho con kịp thời.

Liên hệ bài học với thực tiễn

Để giúp con hiểu rõ hơn về các loại hình tam giác, bố mẹ có thể lấy ví dụ liên quan thông qua các hình ảnh, đồ vật, sự việc gần gũi, xung quanh với bé để con có thể dễ dàng hình dung và ghi nhớ chúng tốt hơn.

Cùng bé thực hành thường xuyên rất quan trọng

Thay vì chỉ học trên sách vở, lý thuyết thì trẻ rất dễ nhanh quên. Chính vì vậy, việc thực hành thường xuyên là rất cần thiết để giúp bé ghi nhớ, áp dụng kiến thức một cách hiệu quả hơn.

Việc thực hành ở đây có thể cùng con làm bài tập trong sách giáo khoa, tìm hiểu thêm nhiều thông tin trên internet để luyện tập, tham khảo nhiều kiến thức nâng cao, tổ chức các trò chơi, cuộc thi, học nhóm cùng bạn bè,…Đảm bảo sẽ nâng cao hiệu quả hơn so với học trên sách vở.