Các kiến thức về hàm số nói chung hay hàm số đồng biến trên r nói riêng là một trong các nền tảng cơ bản trong toán học. Vì thế mà, trong bài viết này, Wikihoc sẽ tập trung giải đáp các câu hỏi như: “Hàm số là gì?”, “Hàm số đồng biến trên r khi nào?”, “Hàm số nghịch biến trên r khi nào?”…
Hàm số là gì?
Giả sử X và Y’ là hai tập hợp tùy ý. Nếu có một quy tắc ƒ cho tương ứng mỗi x ∈ X với một và chỉ một y ∈ Y thì ta nói rằng ƒ là một hàm từ X vào Y, kí hiệu:
ƒ : X → Y
X → ƒ(x)
Nếu X, Y là các tập hợp số thì ƒ được gọi là một hàm số. Trong chương trình Toán 9 chúng ta chỉ xét các hàm số thực của các biến số thực, nghĩa là X ⊂ R và Y ⊂ R. X được gọi là tập xác định (hay miền xác định) của hàm số ƒ. Tập xác định thường được kí hiệu là D.
Số thực x ∈ X được gọi là biến số độc lập (gọi tắt là biến số hay đối số). Số thực y = ƒ(x) ∈ Y được gọi là giá trị của hàm số f tại điểm x. Tập hợp tất cả các giá trị của ƒ(x) khi x lấy mọi số thực thuộc tập hợp X gọi là tập giá trị (hay miền giá trị) của hàm số ƒ.
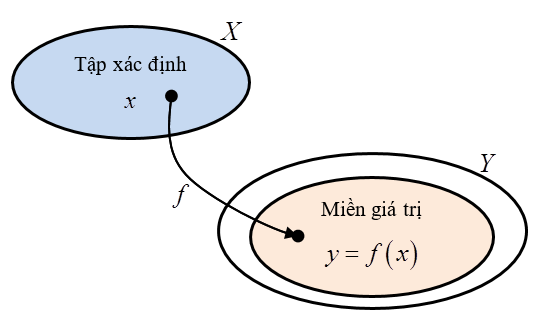
Ta cũng có thể định nghĩa hàm số như sau: Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho: Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x được gọi là biến số.
Khi x thay đổi mà y luôn nhận một giá trị thì y được gọi là hàm hằng. Chẳng hạn, y = 3 là một hàm hằng.
Kí hiệu: Khi y là hàm số của x, ta có thể kí hiệu là y = ƒ(x), hoặc y = g(x) hoặc y = h(x),…
Tập xác định của hàm số y = ƒ(x) là tập con của R bao gồm các giá trị sao cho biểu thức ƒ(x) xác định.
Định lí về tính đồng biến nghịch biến của hàm số
Cho hàm số y = f(x) có đạo hàm trên khoảng (a;b). Khi đó hàm số sẽ đồng biến và nghịch biến với:
– Hàm số y = f(x) đồng biến trên khoảng (a;b) khi và chỉ khi f’(x) ≥ 0 với mọi giá trị x thuộc khoảng (a;b). Dấu bằng xảy ra tại hữu hạn điểm.
– Hàm số y = f(x) nghịch biến trên khoảng (a;b) khi và chỉ khi f’(x) ≤ 0 với mọi giá trị x thuộc khoảng (a;b). Dấu bằng xảy ra tại hữu hạn điểm.
Khi nào hàm số đồng biến trên r? hàm số nghịch biến trên r khi nào?
Trước tiên chúng ta cần biết rằng điều kiện để hàm số đồng biến trên r, điều kiện trước tiên là hàm số phải xác định trên R đã.
Giả sử hàm số y=f(x) xác định và liên tục và có đạo hàm trên R. Khi đó hàm số y=f(x) đơn điệu trên R khi và chỉ khi thỏa mãn hai điều kiện sau:
-
Hàm số y=f(x) xác định trên R.
-
Hàm số y=f(x) có đạo hàm không đổi dấu trên R.
Ở điều kiện thứ 2 để hàm số đồng biến trên r chúng ta cần chú ý là y’ có thể bằng 0 nhưng chỉ được bằng 0 tại hữu hạn điểm (hoặc số điểm mà đạo hàm bằng 0 là tập đếm được).
Một số trường hợp cụ thể chúng ta cần phải nhớ về điều kiện hàm số luôn đồng biến trên r, như sau:
Hàm số đa thức bậc 1

Hàm số đa thức bậc 3

Lưu ý: Hàm số đa thức bậc chẵn không thể đơn điệu trên R được, ví dụ như: Hàm số bậc 2, 4,…
Các dạng bài tập ứng dụng hàm số đồng biến nghịch biến trên r thường gặp
Dưới đây là tổng hợp một số dạng bài tập liên quan tới điều kiện hàm số đồng biến trên r để các em áp dụng và thực hành:
Dạng 1: Tìm khoảng đồng biến – nghịch biến của hàm số
Cho hàm số y = f(x)
-
f’(x) > 0 ở đâu thì hàm số đồng biến ở đấy.
-
f’(x) < 0 ở đâu thì hàm số nghịch biến ở đấy.
Quy tắc:
-
Tính f’(x), giải phương trình f’(x) = 0 tìm nghiệm.
-
Lập bảng xét dấu f’(x)
-
Dựa vào bảng xét dấu và kết luận.
Ví dụ: Cho hàm số f(x) = -2×3 + 3×2 – 3x và 0 ≤ a < b. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên ℝ
B. f (a) > f (b)
C. f (b) < 0
D. f (a) < f (b)
Hướng dẫn giải: Chọn đáp án D.
Ta có: f’(x) = -6×2 + 6x – 3 < 0, ∀ x ∊ ℝ
⇒ Hàm số nghịch biến trên ℝ.
0 ≤ a < b ⇒ f (0) ≥ f (a) > f (b)
Dạng 2: Tìm điều kiện của tham số m
Kiến thức chung
-
Để hàm số đồng biến trên khoảng (a;b) thì f’(x) ≥ 0, ∀ x ∊ (a;b).
-
Để hàm số nghịch biến trên khoảng (a;b) thì f’(x) ≤ 0, ∀ x ∊ (a;b).

Chú ý: Cho hàm số y = ax^3 + bx^2 + cx + d
-
Khi a > 0 để hàm số nghịch biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k
-
Khi a < 0 để hàm số đồng biến trên một đoạn có độ dài bằng k ⇔ y’ = 0 có 2 nghiệm phân biệt x1, x2 sao cho |x1 – x2| = k
Ví dụ: Hàm số y = x3 – 3×2 + (m – 2) x + 1 luôn đồng biến khi:
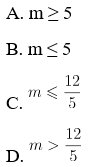
Hướng dẫn giải: Chọn đáp án A.
Ta có: y’ = 3×2 – 6x + m – 2
Hàm số đồng biến trên ℝ khi và chỉ khi y’ = 3×2 – 6x + m – 2 ≥ 0, ∀ x ∊ ℝ
⇔ ∆’ ≤ 0 ⇔ 15 – 3m ≤ 0 ⇔ m ≥ 5
Dạng 3: Xét tính đơn điêu hàm số trùng phương
-
Bước 1: Tìm tập xác định
-
Bước 2: Tính đạo hàm f’(x) = 0. Tìm các điểm xi (i= 1, 2,… n) mà tại đó đạo hàm bằng 0 hoặc không xác định.
-
Bước 3: Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên.
-
Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
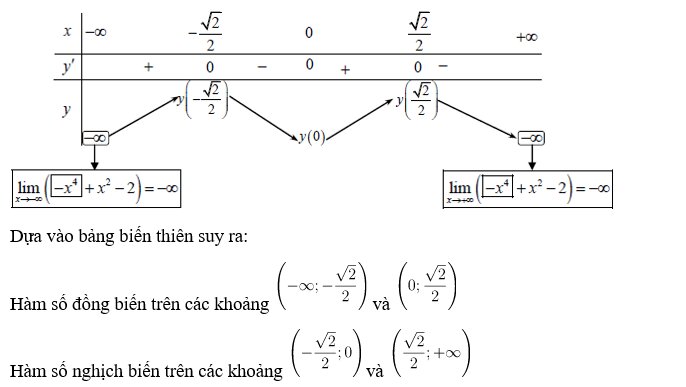
Ví dụ: Xét tính đơn điệu của mỗi hàm số sau: y = -x4 + x2 – 2
Hàm số xác định với mọi x ∊ ℝ
y’ = -4×3 + 2x = 2x (-2×2 + 1)
Cho y’ = 0 ⇒ x = 0 hoặc x = -√2/2 hoặc x = √2/2
Bảng biến thiên:
Các bài tập mẫu khác
Ví dụ 1: Cho hàm số y=x³+2(m-1)x²+3x-2. Tìm m để hàm đã cho đồng biến trên R.
Hướng dẫn giải:
Để y=x³+2(m-1)x²+3x-2 đồng biến trên R thì (m-1)²-3.3≤0⇔-3≤m-1≤3⇔-2≤m≤4.
Các bạn cần lưu ý với hàm đa thức bậc 3 có chứa tham số ở hệ số bậc cao nhất thì chúng ta cần xét trường hợp hàm số suy biến.
Ví dụ 2: Cho hàm số y=mx³-mx²-(m+4)x+2. Xác định m để hàm số đã cho nghịch biến trên R.
Hướng dẫn giải:
Ta xét trường hợp hàm số suy biến. Khi m=0, hàm số trở thành y=-x+2. Đây là hàm bậc nhất nghịch biến trên R. Vậy m=0 thỏa mãn yêu cầu bài toán.
Với m≠0, hàm số là hàm đa thức bậc 3. Do đó hàm số nghịch biến trên R khi và chỉ khi m<0 đồng thời m²+3m(m+4)≤0. Giải các điều kiện ra ta được -3≤m<0.
Kết hợp 2 trường hợp ta được -3≤m≤0 thỏa mãn yêu cầu bài toán.
Một số bài tập tính hàm số đồng biến trên r và nghịch biến trên r tự luyện

Trên đây là tất cả các kiến thức và dạng bài tập về hàm số đồng biến trên r. Bên cạnh đó Wikihoc còn bổ sung thêm các định nghĩa về hàm số nói chung và các dạng hàm số nói riêng như: Hàm số bậc nhất, hàm số bậc hai,… Hàm số lượng giác, hàm số logarit và hàm số mũ. Hy vọng với những chia sẻ trên đây của Wikihoc sẽ giúp bạn phần nào trong việc ôn tập và ghi nhớ các kiến thức cần thiết trong các kì thi, đặc biệt là kì thi THPT Quốc Gia. Xin được đồng hành cùng bạn.
