Đạo hàm tại 1 điểm là một trong những dạng đạo hàm cơ bản, nhưng nhiều học sinh vẫn chưa nắm được bản chất và cách giải bài tập vận dụng. Vậy nên, nội dung bài viết sau sẽ hướng dẫn cách giải bài tập về dạng đạo hàm này chi tiết nhé.
Đạo hàm tại 1 điểm là gì?
Đạo hàm tại 1 điểm được biết đến là một trong những dạng đạo hàm cơ bản trong chương trình lớp 11 các học sinh sẽ được học.

Công thức tính đạo hàm liên tục tại 1 điểm
Để có thể giải được các bài tập liên quan tới đạo hàm của 1 điểm đòi hỏi học sinh phải nắm rõ công thức và cách tính đơn giản dựa vào định nghĩa trên. Vậy nên, sau đây là công thức chi tiết để mọi người tham khảo:

Các dạng bài tập thường gặp về đạo hàm tại 1 điểm và cách giải
Trong bài toán về đạo hàm nói chung, đạo hàm tại 1 điểm nói riêng sẽ có những dạng toán riêng tương ứng với những bài tập và phương pháp giải riêng. Đòi hỏi học sinh phải nhận biết được các dạng, để từ đó có thể áp dụng công thức, phương pháp giải phù hợp và đảm bảo chính xác nhất.
Vậy nên dưới đây là một số dạng bài tập thường gặp về toán đạo hàm ở 1 điểm và phương pháp giải chi tiết mà học sinh có thể tham khảo và áp dụng:
Dạng 1: Tính đạo hàm theo định nghĩa

Ví dụ: y = x2 + x tại x0 = 1
–> Cách giải:
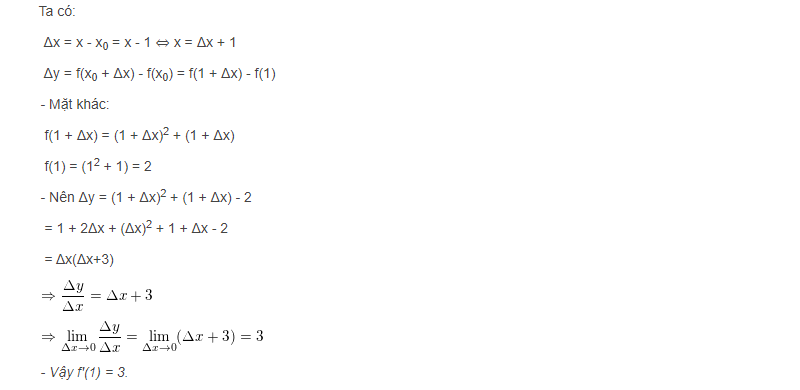
Dạng 2: Liên hệ giữa đạo hàm và tính liên tục của hàm số
Đây là một trong những dạng toán cơ bản thường gặp nhất khi làm toán đạo hàm ở 1 điểm, chúng thường xuất hiện trong các kỳ thi nên các em cần phải lưu ý để áp dụng đúng phương pháp giúp giải bài tập chính xác.

Ví dụ:Chứng minh rằng hàm số

Không có đạo hàm tại điểm x = 0 nhưng chúng lại có đạo hàm tại điểm x = 2.
–> Cách giải
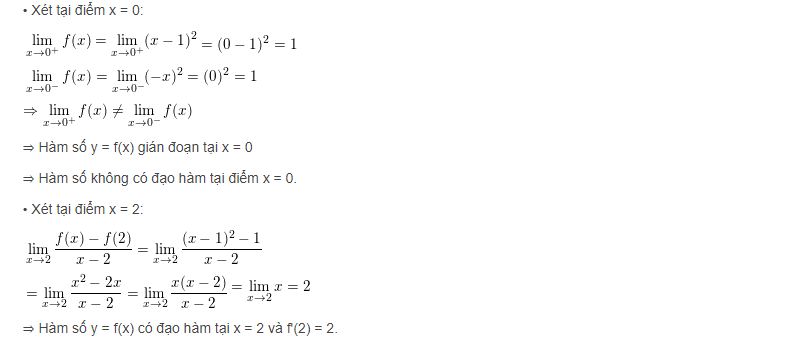
Dạng 3: Viết phương trình tiếp tuyến tại 1 điểm M0 (X0;f(X0)) ∈ (C)
Dạng toán đạo hàm tại 1 điểm dưới dạng viết phương trình tiếp tuyến sẽ có hơn so với những dạng toán trên, đòi hòi các học sinh phải nắm rõ phương pháp giải chi tiết của từng bài toán để đảm bảo tính chính xác. Cụ thể:
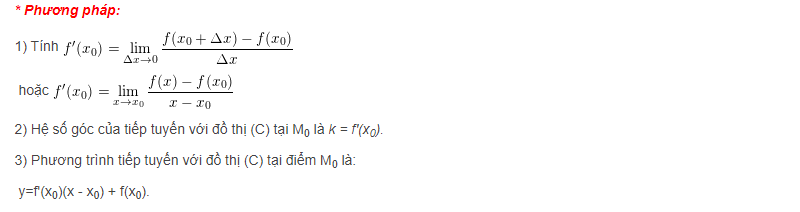
Ví dụ: Viết phương tiếp tuyến đường cong y = x3
a) Tại điểm (-1;-1)
b) Tại điểm có hoành độ tương ứng bằng 2.
–> Cách giải:

Dạng 4: Viết phương trình tiếp tuyến với đồ thị (C) khi biết hệ số góc K
Đây là một trong những dạng toán đạo hàm ở 1 điểm nâng cao, học sinh sẽ phải nắm rõ công thức tính kết hợp với phương pháp giải phương trình tiếp tuyến trên cùng với đồ thị (C) và phương trình hệ số góc k để tìm được đáp án chính xác. Phương pháp giải cụ thể như sau:

Ví dụ: Viết phương trình tiếp tuyến đường cong y = x3. Biết hệ số góc tương ứng của tiếp tuyến đó bằng 3.
–> Cách giải:
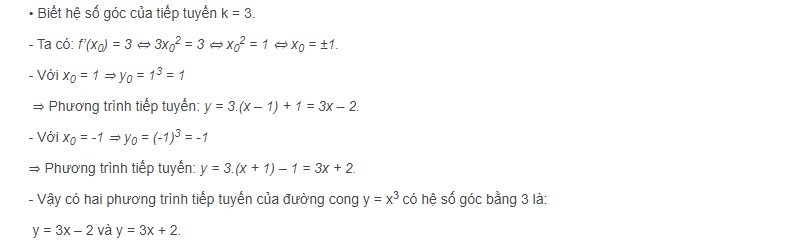
Một số bài tập tự luyện tính đạo hàm tại 1 điểm tự luyện
Có thể bạn chưa biết, dạng toán tính đạo hàm ở 1 điểm là dạng kiến thức cơ bản nhưng cũng khá khó trong chương trình toán 11. Đồng thời, kiến thức này sẽ xuất hiện ở mọi mặt trận các kỳ thi từ học kỳ, học sinh giỏi, THPT và kể cả đại học.
Chính vì vậy, để không bỏ qua điểm ở dạng bài tập này đòi hỏi các em ngoài việc nắm vững các công thức, dạng bài tập và phương pháp giải cần phải thực hành luyện tập nhiều hơn.
Vậy nên, sau đây là những mẫu bài tập về đạo hàm tại 1 điểm để các em có thể tham khảo và tự luyện thuần thục hơn nhé:

Tìm hiểu thêm: Nguyên hàm lượng giác: Khái niệm, công thức, mẹo giải và bài tập chi tiết
Kết luận
Trên đây là tổng hợp những kiến thức về toán đạo hàm tại 1 điểm. Qua đó có thể thấy chúng có những điểm khó và điểm dễ riêng khi làm. Quan trọng các em cần phải nắm vững công thức và phương pháp giải mà Wikihoc chia sẻ trên hoàn toàn có thể chinh phục được các bài tập và chiếm trọn điểm thi ở dạng câu hỏi này. Chúc các em thành công.
