Đạo hàm logarit là một trong những phần kiến thức trọng điểm được xếp vào bộ đề thi THPT Quốc Gia. Do đó, các bạn học sinh cần chủ động học tập và ôn luyện thường xuyên để không còn bỡ ngỡ khi gặp phải các dạng bài thuộc nội dung này. Vậy, bài viết sau đây, Wikihoc sẽ giúp bạn dễ dàng làm chủ được đạo hàm log nhé!
Đạo hàm là gì? Các công thức đạo hàm của một số hàm cơ bản
Khái niệm và cách tính đạo hàm tại một điểm
Đây được coi là phần kiến thức cơ bản nhưng cần nắm thật chắc để học được các nội dung cao cấp hơn sau này. Theo đó, trong chương trình toán giải tích, đạo hàm của một hàm số được định nghĩa là sự biến thiên của hàm tại một điểm bất kỳ cho trước. Từ đây, ta có được phần khái niệm chi tiết như sau:

Dựa vào đây, một cách tính đạo hàm đã được xây dựng để bạn có thể dễ dàng áp dụng và có được ra kết quả cần tìm. Công thức bao gồm 3 bước chính:
-
Bước 1: Ta giả sử x là số gia của đối số tại điểm x0. Từ đó biến đổi để được như sau: y=f(x0+x)−f(x0)
-
Bước 2: Tỷ số được lập sẽ là (delta y)/ (delta x)
-
Bước 3: Cũng là bước cuối cùng trong cách tìm đạo hàm dựa trên khái niệm đã cho. Cụ thể, ta tính lim(delta x ->0)=(delta y)/ (delta x)
Tổng hợp công thức đạo hàm của một số hàm cơ bản
Ngoài ra, chúng ta còn có các công thức đã được chứng minh và cho phép học sinh áp dụng để tính đạo hàm của một số hàm cơ bản. Như vậy, bạn cần học thuộc cũng như hiểu được bản chất của những công thức cho sẵn này. Nhờ đó, học sinh sẽ linh hoạt trong từng dạng bài tập và nhanh gọn hơn trong mỗi bước tính toán.
Dưới đây, Wikihoc tổng hợp lại bảng các công thức đạo hàm thông dụng. Và thường gặp nhất của hàm sơ cấp và hàm hợp trong nội dung học giải tích.

Định nghĩa và tính chất đạo hàm logarit
Vậy là chúng ta đã biết được khái niệm của đạo hàm là gì. Bên cạnh đó là những công thức tìm đạo hàm của hàm sơ cấp và hàm hợp mà học sinh thường gặp.
Các bạn hãy học thuộc cũng như thật kỹ phần kiến thức trên trước khi chuyển sang nội dung về logarit đạo hàm với nhiều dạng khó và phức tạp hơn nhé. Ngay dưới đây, Wikihoc sẽ cung cấp đến học sinh về định nghĩa cũng như công thức tính của log x đạo hàm nhé!
Đạo hàm logarit là gì?
Hiểu một cách đơn giản, hàm logarit là một hàm số được biểu diễn dưới dạng logarit. Cụ thể, với số thực a cho trước (a>0; a≠1; x>0), ta có hàm số y=logax được định nghĩa là hàm số logarit cơ số a. Từ đây, đạo hàm hàm số logarit trên có công thức y’=1/xlna.
Tính chất đạo hàm logarit
Đây là các tính chất của đạo hàm logarit cơ bản được áp dụng nhiều trong các dạng bài khác nhau. Học sinh chú ý ghi nhớ để tính thành thạo đạo hàm log.
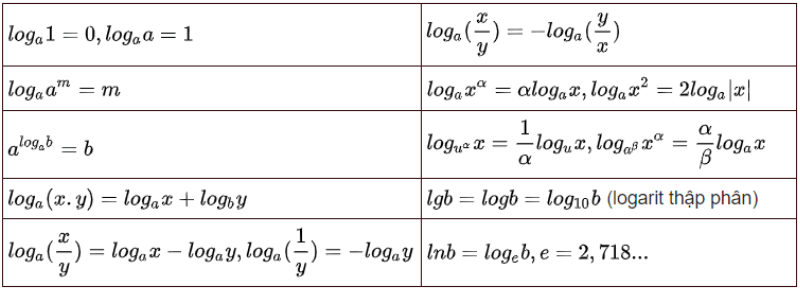
Bảng đạo hàm logarit đầy đủ và chi tiết nhất
Vậy là các bạn và Wikihoc đã cùng nhau học về khái niệm đạo hàm của hàm logarit. Tiếp theo, chúng mình sẽ tìm hiểu về bảng đạo hàm logarit mà Wikihoc đã tổng hợp và chọn lọc một cách đầy đủ cũng như chính xác nhất.
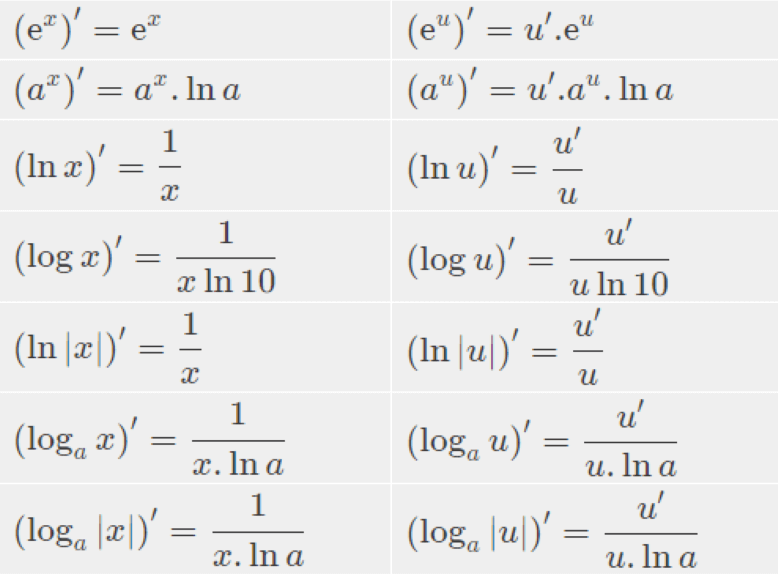
Lưu ý, để giúp ghi nhớ tốt hơn trong quá trình học, các bạn học sinh hãy tự tìm ra phương pháp tốt nhất cho bản thân. Chẳng hạn như, ghi công thức vào giấy nhớ và dán trên gương hay mặt bàn để nhìn thấy mỗi ngày.
Hoặc đề ra cho bản thân mục tiêu học thuộc 2 công thức đạo hàm logarit mỗi ngày. Nhờ đó, bạn sẽ có động lực và sự quyết tâm thúc đẩy bản thân đến khi nhớ được đầy đủ bảng đạo hàm log x.
Xem thêm: Đạo hàm là gì? Khái niệm và công thức đạo hàm từ cơ bản đến nâng cao
Một số dạng bài tập đạo hàm logarit thường gặp có lời giải
Để học thuộc được các công thức đạo hàm logarit đã khó, việc biết cách làm và áp dụng trong quá trình giải toán còn thách thức học sinh nhiều hơn. Do đó, bạn nên kết hợp giữa ghi nhớ công thức và luyện tập thường xuyên với nhiều dạng bài tập khác nhau để hình thành nên thói quen tính đạo hàm logarit.
Dưới đây là một số dạng bài tập chính thường gặp trong khi giải đề mà Wikihoc cung cấp đến học sinh. Các bạn hãy tham khảo và thử tìm nhiều cách tính khác cho mỗi bài đạo hàm log(u) nhé!
Dạng 1: Tìm tập xác định của đạo hàm hàm số logarit
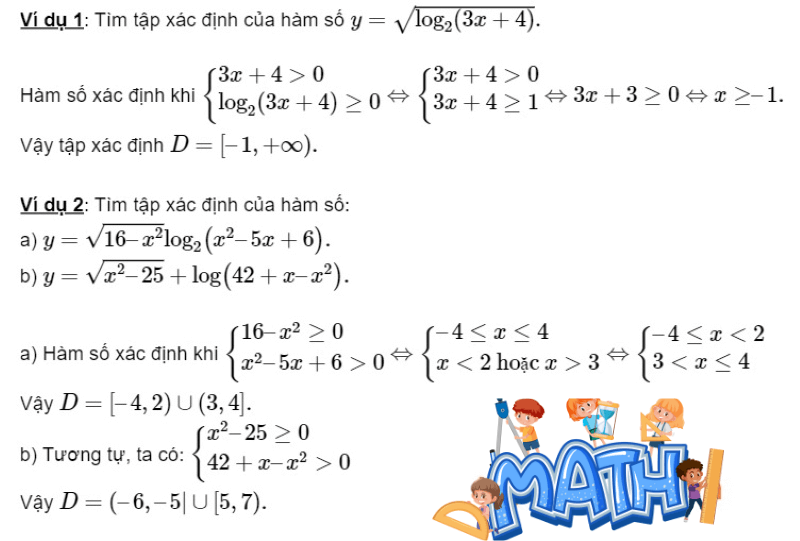
Dạng 2: Khảo sát đồ thị đạo hàm logarit



Dạng 3: Tính đạo hàm của hàm số logarit

Cách bấm máy tính đạo hàm logarit đơn giản nhất
Một ứng dụng rất hay của máy tính cầm tay đó là hỗ trợ học sinh trong cách tính đạo hàm logarit. Chỉ bằng vài thao tác đơn giản, bạn đã có cho mình kết quả của những bài tập đạo hàm hàm số logarit cơ bản và định hướng làm đối với những bài nâng cao hơn. Hãy cùng khám phá ngay cách bấm máy đạo hàm logarit dưới đây.

Như vậy, khi làm đề thi trắc nghiệm THPT Quốc Gia, các bạn học sinh hãy sử dụng bấm máy tính đạo hàm logarit để cho ra kết quả nhanh và chính xác hơn. Ngoài ra, bạn có thể tham khảo các video trên youtube hay bài giảng của thầy cô để học thêm nhiều mẹo hay ho khi giải đạo hàm logarit bằng máy tính.
Thông qua bài viết trên, Wikihoc đã cung cấp đến bạn đọc về khái niệm, công thức đạo hàm logarit và những dạng bài tập thường gặp nhất. Bên cạnh đó, chúng mình cũng được học về cách bấm máy tính để đơn giản hóa quá trình giải đạo hàm logarit nepe. Hy vọng, với những kiến thức bổ ích này, học sinh sẽ ôn luyện chăm chỉ mỗi ngày để đạt kết quả tốt nhất.
