Đạo hàm lượng giác là những hàm số tuyến tính được ứng dụng nhiều trong hình học và vật lý. Tuy nhiên, những hàm này khá khó nhớ, đặc biệt là đạo hàm arctan x, gây khó khăn cho người học. Vậy để có thể hiểu và nhớ lâu hơn, ta cần phải hiểu được bản chất của nó cũng như phải thường xuyên luyện tập. Cùng tìm hiểu về đạo hàm của arctan x qua bài viết sau nhé!

Hàm số y = arctan x là gì?
Để tìm hiểu về đạo hàm arctan x, đầu tiên ta cần hiểu về công thức hàm số gốc của nó là y = arctan x. Vậy hàm số y = arctan x là gì? Cùng tìm hiểu về định nghĩa, hình dáng đồ thị và các quy tắc cần nhớ của hàm số này ngay sau đây nhé!
Định nghĩa
Về định nghĩa, hàm số y = arctan x là hàm tiếp tuyến ngược của x khi x thuộc tập hợp số thực ( x=R). Với hàm tiếp tuyến của y bằng x có công thức là tan y = x thì khi đó arctan của x sẽ bằng hàm tiếp tuyến ngược của x với công thức y = arctan x = tan ^(-1) . x
Lấy ví dụ: Cho y = arctan x với x bằng 1. Suy ra y = arctan 1 = tan ^(-1). 1 = π / 4 rad = 45 °
Hình dáng đồ thị
Đồ thị của hàm số y = arctan x hay còn gọi f (x) = arctan x có dạng đường cong tiếp tuyến đối xứng qua trục tọa độ. Hàm số nằm ở góc phần tư thứ nhất và thứ 3, cách đều với trục tung.
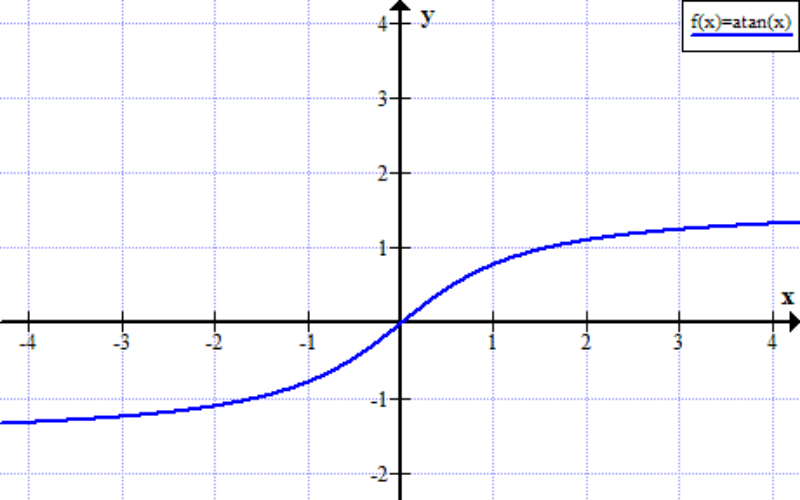
Quy tắc cần nhớ
Để vận dụng được hàm số y = arctan x trong giải toán, ta cần phải nắm rõ các quy tắc arctan để có thể vận dụng một cách linh hoạt nhất. Bảng dưới đây chúng tôi đã hệ thống lại các quy tắc cần nhớ của hàm số này.
Quy tắc Arctan
Công thức tính đạo hàm của hàm số y = arctan x
Trong toán học, ngoài các bài toán có kết quả giới hạn thì cũng có vô số các bài toán thuộc tập hợp vô hạn, có nghĩa là tập hợp chạy đến vô cùng. Điều này đặt ra rằng ta cần phải tìm giới hạn của các tập hợp số đó. Từ đó mà ta xuất hiện các khái niệm giới hạn lim và các công thức đạo hàm.
Đạo hàm được định nghĩa là tỉ số giữa số gia của hàm số đó với số gia của đối số đó tại điểm cụ thể là x0, khi đó thì số gia đối số tiến sát đến 0 chính là đạo hàm của hàm y = f (x) tại x0. Đạo hàm được ứng dụng nhiều trong việc giải bài toán lượng giác, các bài toán thực tế về các lĩnh vực vật lý, hoá học, sinh học hay kỹ thuật, đặc biệt là đạo hàm arctan x.
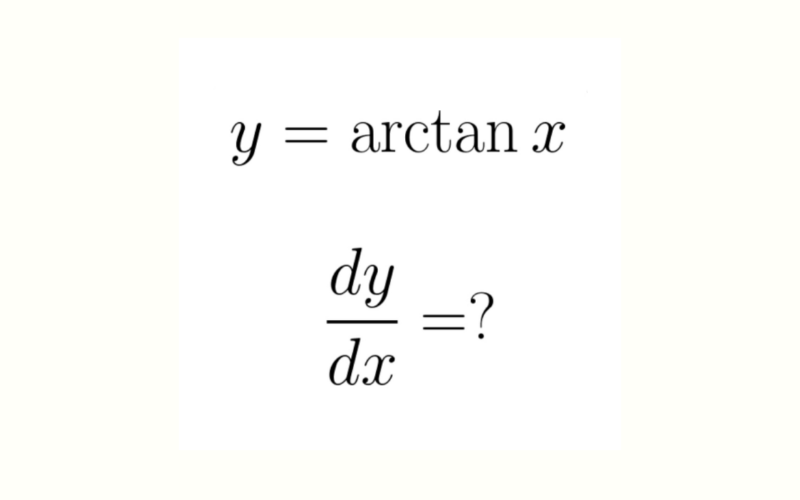
Quy tắc tính đạo hàm nói chung
Nói về quy tắc tính đạo hàm tức là nói đến cả một hệ thống các quy tắc tổng quan nhất mà bạn cần phải nhớ. Có như vậy sau này bạn mới có thể hiểu và xây dựng được các công thức tính đạo hàm từ cơ bản đến nâng cao, ví dụ như đạo hàm arctan x.
Hệ thống quy tắc tính đạo hàm gồm 6 quy tắc dưới đây:
-
Quy tắc đạo hàm về cộng, trừ nhiều hàm số: (u + v – w )’ = u’ + v’ – w’
-
Quy tắc đạo hàm về hằng số: (ku)’ = ku’ trong đó k là hằng số, u là hàm số
-
Quy tắc đạo hàm về phép nhân hai hàm số (u.v)’ = u’.v + u.v’
-
Quy tắc đạo hàm của phân số (u/v)′=(u′v – uv’)/v^2
-
Quy tắc đạo hàm của hàm ngược(1/v)′=−v′/v^2
-
Quy tắc đạo hàm của hàm hợp dạng y(u(x): [y(u(x))]’ = [y(u)]’.[u(x)]’
Trong đó, với ký hiệu dấu phẩy trên có nghĩa là ký hiệu đạo hàm. Các ký hiệu u; v ; w là các hàm số u = u(x); v = v(x); w = w(x).
Xem thêm: Công thức tính đạo hàm arctan u và các dạng bài tập tự luyện
Cách tính đạo hàm của hàm số y = arctan x
Ở các phần trên, chúng tôi đã giới thiệu cơ bản về hàm số y = arctan x và các quy tắc tính đạo hàm. Vậy thì đạo hàm của hàm số y = arctan x là gì? Nó có cách tính như thế nào? Cùng tìm hiểu ngay ở phần này nhé!
Để tính được đạo hàm của hàm số y = arctan x, ta sử dụng từ định nghĩa hàm arctan x.
Với tan y = x, lấy đạo hàm 2 vế theo biến x, ta được:
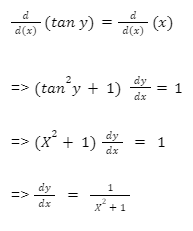
Từ đó suy ra cách tính đạo hàm của hàm số y = arctan x là:
![]()
Một số dạng bài tập để tự luyện
Trên đây là cách chứng minh cho công thức của đạo hàm arctan x. Để hiểu sâu hơn và có thể vận dụng thực tế, chúng ta cùng đi đến với một số dạng bài tập để tự luyện cơ bản như là:
-
Luyện tính đạo hàm của hàm số y = arctan x theo định nghĩa như đã trình bày ở trên.
-
Các bài tập có liên quan đến các công thức tính đạo hàm, tìm giới hạn lim của hàm số để quen với dạng toán tính đạo hàm. Từ đó vận dụng vào các bài toán có số liệu arctan.
-
Vận dụng trong các bài tập thực tế về tính quãng đường, gia tốc trong vật lý.
Đạo hàm arctan x là một công thức đạo hàm quan trọng và khá khó nhớ. Vì vậy, để có thể nhớ được lâu, ta cần phải thực sự hiểu về nó và luyện tập nó thường xuyên. Qua bài viết này, chúng tôi hy vọng đã cung cấp cho bạn những kiến thức bổ ích về đạo hàm arctan.
