Trong toán học có rất là nhiều công thức khác nhau, đặc biệt đạo hàm arctan là một trong những công thức phổ biến nhất ở trong hàm lượng giác. Vậy, để giúp các bạn hiểu và nắm rõ về các công thức này, sau đây là một số dạng bài mẫu về đạo hàm của arctan mà bạn có thể tham khảo.
Tổng quát về đạo hàm của hàm arctan
Arctan chính là một hàm số ngược ở trong công thức đạo hàm lượng giác của toán học. Hay còn có thể gọi là căn thức của hàm số tan.
Ngoài ra, để tồn tại hàm số ngược thì hàm số đó phải đáp ứng một trong các điều kiện sau đây:
-
Mệnh đề 1: Hàm f (X -> Y) có hàm ngược khi và chỉ khi f chính là ánh xạ 1-1 từ X vào Y.
-
Mệnh đề 2: Hàm f (X -> Y) có hàm ngược ở trên khoảng (a,b) nếu như f là đơn điệu tăng hoặc giảm chặt trên (a,b).
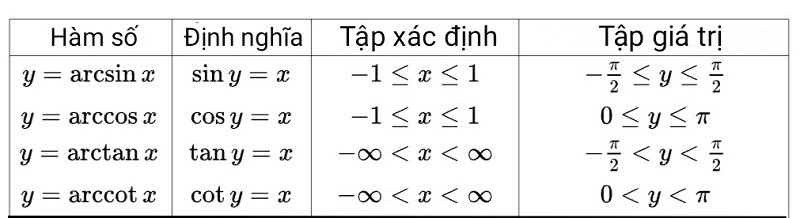
Các công thức tính đạo hàm arctan thường gặp
Hiện nay có rất nhiều công thức đạo hàm arctan từ đơn giản cho đến nâng cao. Tuy nhiên, đối với chương trình giáo dục cơ bản gần đây thì thường chỉ sử dụng một số công thức đạo hàm arctan sau đây.
Công thức tính đạo hàm của hàm số y = arctan x
Hàm số y = arctan x là một hàm tiếp tuyến ngược của x khi và chỉ khi x thuộc tập hợp số thực. Lúc này, khi hàm của y bằng x và có công thức là tan y = x thì arctan x sẽ là hàm tiếp tuyến ngược của x.
Đây là một trong những công thức đạo hàm arctan phổ biến nhất, để giúp các bạn dễ hiểu hơn. Sau đây là công thức và ví dụ mà bạn có thể tham khảo.
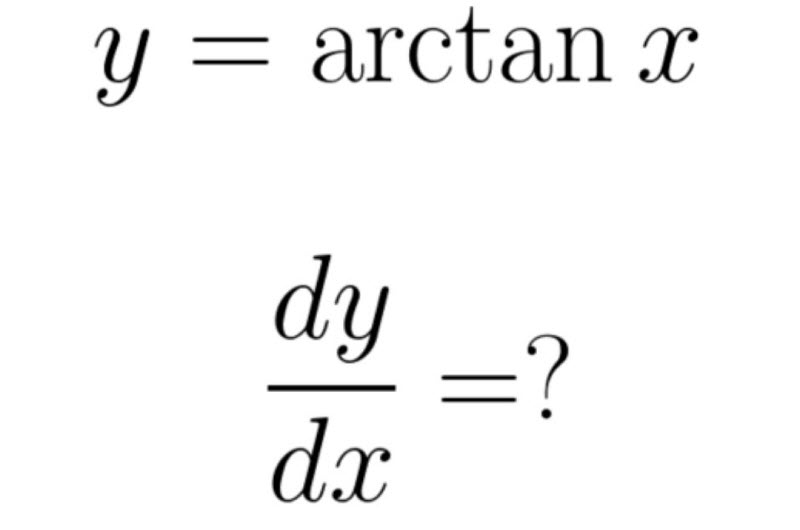
Công thức
Cho hàm số: y=arctan x
Trong đó:
![]()
Thì ta có: tan y = x
Dùng đạo hàm ẩn rồi giải dy/dx ta được:
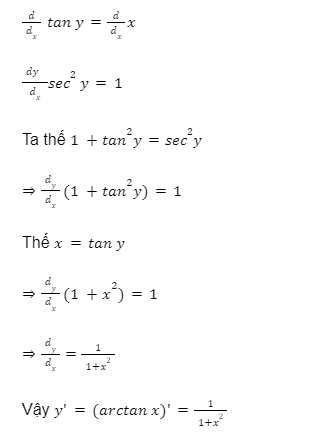
Ví dụ
Tính đạo hàm của y = arctan x
Lời giải:
Từ định nghĩa của hàm arctan và y = arctan x ta có tan y = x. Lấy đạo hàm theo biến x ta được phương trình như sau:
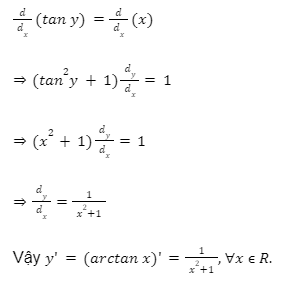
Công thức tính đạo hàm của arctan(u)
Đây chính là hàm hợp của hàm số arctan x . Vì vậy bạn có thể dễ dàng suy ra công thức của hàm số này như sau.
Công thức
![]()
Ví dụ
Tương tự như hàm số y = arctan x được cung cấp ở trên các bạn hãy tìm đạo hàm arctan của hàm số sau y = x^2.arcsin(x)
Lời giải:
Vận dụng lý thuyết của đạo hàm ngược, ta có:
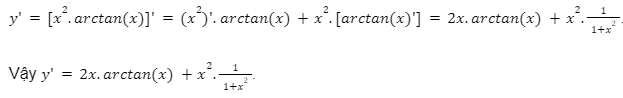
Công thức tính đạo hàm arctan x/y
Đây cũng chính là một trong những công thức mà các bạn sẽ thường gặp trong đạo hàm của arctan. Để giúp các bạn hiểu rõ hơn thì sau đây sẽ là công thức và ví dụ.
Công thức
![]()
Ví dụ
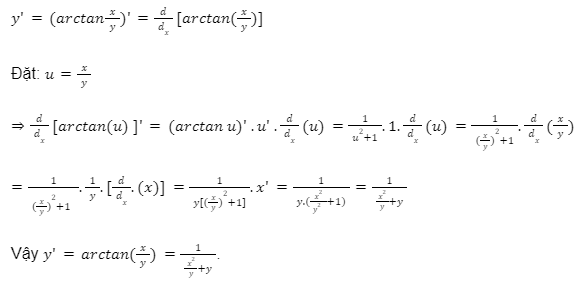
Xem thêm: Cực trị của hàm số: Chi tiết lý thuyết và các dạng bài tập thường gặp
Một số mẫu bài tập tự luyện có lời giải
Để giúp các bạn làm quen được các dạng bài đạo hàm của arctan, sau đây là một số bài tập mẫu tự luyện ở nhà có lời giải mà bạn có thể tham khảo.
Bài tập 1: Tìm đạo hàm của những hàm số sau.
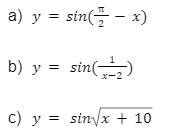
Lời giải:
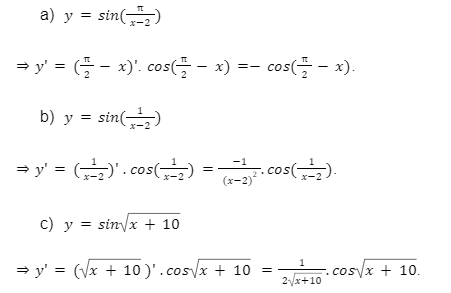
Bài tập 2: Tìm đạo hàm của những hàm số sau.
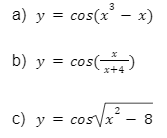
Lời giải:
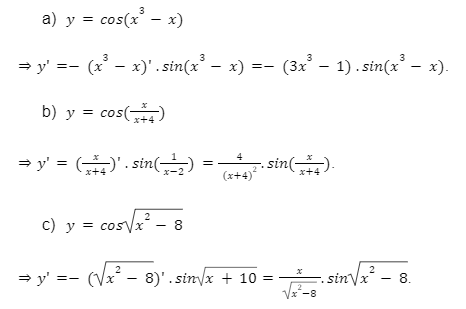
Bài tập 3: Tính đạo hàm của những hàm số sau:
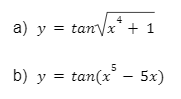
Lời giải:
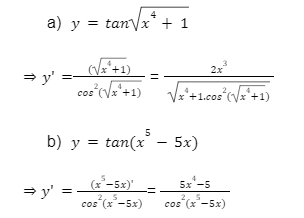
Bài tập 4: Tính đạo hàm của những hàm số sau:
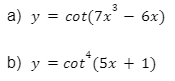
Lời giải:
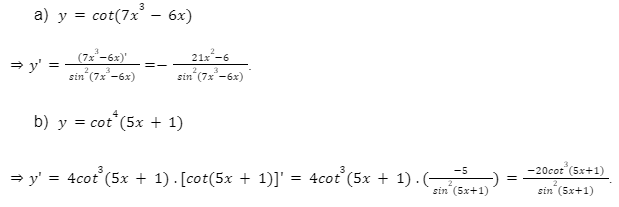
Bài tập 5: Tính đạo hàm của hàm số sau:
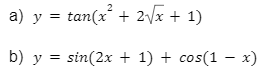
Lời giải:
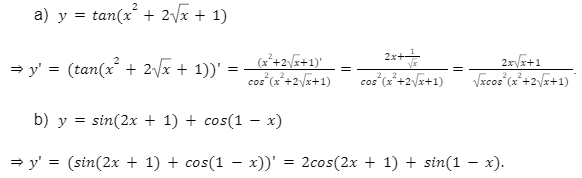
Bài tập 6: Đạo hàm của các hàm số sau bằng bao nhiêu?
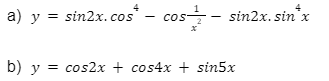
Lời giải:
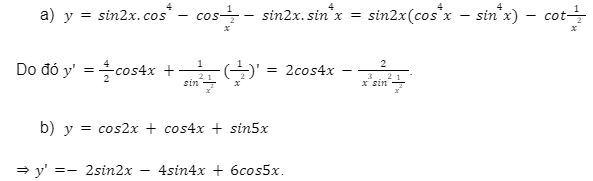
Trên đây là những dạng đạo hàm arctan phổ biến nhất mà bạn có thể gặp. Hy vọng với những thông tin được cung cấp trong bài viết sẽ giúp cho bạn học và làm bài tập đạt được kết quả tốt nhất.
