Đạo hàm trị tuyệt đối được xem là một trong những dạng bài tập đòi hỏi sự tập trung và nắm bắt chắc gốc rễ của toán học cơ bản; từ đó mới có thể hình dung chi tiết các dạng biến đổi của hàm số khi tiến về 0. Vì tính chất phức tạp của dạng bài này trong chương trình học, đạo hàm được xem là một trong cửa ải căm go cho người học.
Tuy nhiên, thông qua sự tổng hợp kiến thức đạo hàm mà Wikihoc cung cấp sau đây, tin chắc rằng học sinh và các sĩ tử lớp 12 có thể nắm bắt ngay dạng toán này và vận dụng chúng một cách thành thục.
Đạo hàm trị tuyệt đối là gì?
Đạo hàm giá trị tuyệt đối là một công thức toán học được dùng để tính toán giá trị tuyệt đối của một giá trị (một con số) trong đạo hàm. Trước tiên để có cái nhìn tổng quát về đạo hàm của trị tuyệt đối, cần nắm bắt chi tiết đạo hàm là gì.
Vậy đạo hàm là gì? Đạo hàm là một phép tính mà ở đó giá trị x0 có số gia của đối số tiến dần về 0. Lúc đó, ta sẽ gọi là đạo hàm của hàm số y = f(x) tại điểm x0.
Ví dụ:
![]()
Hoặc ![]()
Trong đó:
-
Số gia của đối số là: ∆x=x – x0
-
Số gia của hàm số là: ∆y=y – y0
Dựa vào công thức đạo hàm ban đầu, ta sẽ bắt đầu tính hàm số y = |x|
![]()
Thay giá trị |x| vào, ta sẽ tính đạo đạo hàm của y’ bằng cách:
![]()
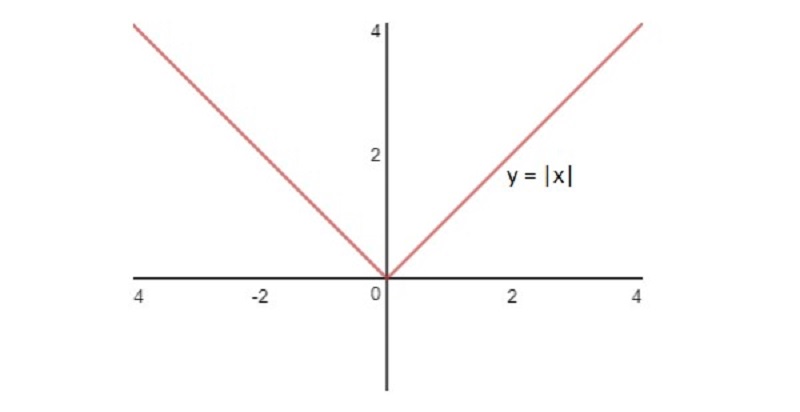
Nhìn vào công thức đạo hàm ở trên, các em thấy rằng đạo hàm sẽ không xác định được tại vị trí ∆x=0, bởi vì hàm số y=|x| là 1 hàm số không liên tục và có dạng:
-
y= x nếu x >= 0
-
y= -x nếu x < 0
Nhìn vào đồ thị y = |x| sẽ giúp bạn đọc dễ hình dung vị trí của y = |x| và xác định đúng giá của của |x|:
Các công thức tính đạo hàm hàm số chứa trị tuyệt đối
Để giúp cho học sinh cũng như các bậc phụ huynh tìm ra giải pháp nhanh nhất cho các bài toán đạo hàm trị tuyệt đối của x phức tạp, Wikihoc xin giới thiệu công thức tính đạo hàm hàm số chứa giá trị tuyệt đối siêu nhanh mà ai cũng nên trang bị sẵn cho mình.
Công thức chung của đạo hàm hàm số chứa trị tuyệt đối
Sau đây sẽ là một vài công thức đạo hàm trị tuyệt đối x cơ bản nhằm mục đích giúp người học tập nhận biết, áp dụng đúng công thức cho mỗi phương trình khác nhau. Cuối cùng là, tập luyện nâng cao dựa trên các kiến thức đạo hàm hàm trị tuyệt đối tổng quát.

Công thức tính đạo hàm trị tuyệt đối của |x| là gì?
Dựa vào công thức đạo hàm ban đầu, ta sẽ bắt đầu tính hàm số y=x
![]()
Thay giá trị x vào, ta sẽ tính đạo đạo hàm của y’ bằng cách:
![]()
Nhìn vào công thức đạo hàm ở trên, các em thấy rằng đạo hàm sẽ không xác định được tại vị trí ∆x=0, bởi vì hàm số y=|x| là 1 hàm số không liên tục và có dạng:
-
y= x nếu x >= 0
-
y= -x nếu x < 0

Đến bước này, ta có thể áp dụng các công thức cộng trừ nhân chia thông thường để tìm ra đáp án cuối cùng cho phương trình:


Tóm gọn lại, ví dụ sau đây cũng chính là cách thức tính đạo hàm giá trị tuyệt đối cơ bản cho một hàm số y=|x|.
Xem thêm: Tất tận tật kiến thức về đạo hàm căn: Căn bậc 3, căn u, căn x, căn logarit,…
Một số công thức tính nhanh đạo hàm trị tuyệt đối
Các công thức tính đạo hàm của hàm trị tuyệt đối:
-
Hàm số phân thức bậc nhất:
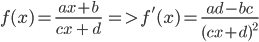
-
Hàm số phân thức bậc hai:
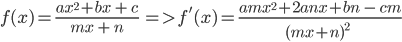
-
Hàm số đa thức bậc ba:
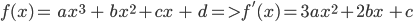
-
Hàm số trùng phương:
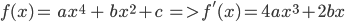
-
Hàm số chứa căn bậc hai:
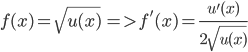
-
Hàm số chứa trị số tuyệt đối:
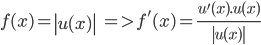
Một số dạng bài tập tự luyện thường gặp
Để giúp học sinh củng cố bài học, sau đây sẽ là những bài tập cơ bản của đạo hàm của giá trị tuyệt đối. Quý phụ huynh có thể tham khảo ngay sau đây. Mục đích chính của các bài tập này là giúp học sinh tiếp cận với công thức đạo hàm trị tuyệt đối; đồng thời củng cố kiến thức cho các sĩ tử sắp sửa phải đối đầu với kỳ thi THPT quan trọng.

Hy vọng rằng, Wikihoc đã giúp bạn hình dung và nắm bắt rõ các kiến thức cơ bản nhất của đạo hàm trị tuyệt đối. Nắm chắc kiến thức, bình tĩnh làm bài và vượt qua các thử thách đạo hàm trước mặt ngay nào! Wikihoc hân hạnh là người đồng hành cùng các bạn trong chặng đường giải toán phía trước.
