Nguyên hàm hữu tỉ là một dạng nguyên hàm cơ bản mà mọi người sẽ được học trong chương trình toán lớp 12. Vậy nguyên hàm hữu tỉ là gì? Công thức và cách giải ra sao? Hãy cùng Wikihoc tìm hiểu rõ hơn ngay trong bài viết sau đây nhé.
Nguyên hàm hữu tỉ là gì?
Về cơ bản, đây là một dạng toán nguyên hàm thường gặp trong chương trình toán học GDPT bậc THPT.
Trước khi hiểu định nghĩa về nguyên hàm hữu tỉ, học sinh cần phải nắm rõ thế nào là hàm hữu tỉ. Thực chất đây còn được gọi là hàm phân thứcbao gồm những số hữu tỉ được viết dưới dạng phân số. Nghĩa là một hàm số hữu tỉ có thể được biểu diễn bằng một số thập phân vô hạn tuần hoàn.
Còn nguyên hàm hữu tỉ cũng sẽ bao gồm các hàm số hữu tỉ kết hợp với nguyên hàm có dạng có dạng: .
Trong đó, P và Q là những đa thức đối với x, còn Q không phải là một đa thức không. Tập xác định của f chính là tập hớp các điểm x tại mẫu thức Q(x) khác 0.
Tất cả các đa thức đều là nguyên hàm đa thức đều là hàm số hữu tỉ với Q(x) = 1. Một nguyên hàm không viết dưới dạng phân thức trên sẽ không phải là nguyên hàm hữu tỉ.
Công thức nguyên hàm hữu tỉ chi tiết nhất
Việc nắm rõ khái niệm chủ yếu giúp học sinh hiểu rõ về bản chất của nguyên hàm các số hữu tỉ, còn để giải các bài toán liên quan sẽ cần phải có công thức cụ thể.

Lưu ý: Trên đây là công thức tính nguyên hàm các hàm số hữu tỉ cơ bản, được ứng dụng trong các dạng toán cơ bản. Tuy nhiên, học sinh cũng cần phải nắm rõ chúng để có thể vận dụng giải các bài toán nâng cao tùy vào tính chất của từng bài toán khác nhau.
Các dạng bài tập về nguyên hàm hữu tỉ thường gặp và cách giải
Đối với toán nguyên hàm hàm số hữu tỉ sẽ có nhiều dạng bài tập khác nhau, trong đó phổ biến nhất là 4 dạng sau đây:

Một số phương pháp tính hàm số hữu tỉ đơn giản
Để giúp học sinh có thể áp dụng các dạng toán tìm nguyên hàm hàm số hữu tỉ chính xác, nhanh chóng hơn thì dưới đây là một số phương pháp mà các em có thể tham khảo:
Tìm nguyên hàm của hàm số hữu tỉ bằng phương pháp chia đa thức
Đối với dạng toán tìm nguyên hàm hàm số hữu tỉ theo phương pháp chia đa thức sẽ giúp giải quyết bài toán nhanh và chính xác hơn theo công thức sau:

Để áp dụng phương pháp giải dạng toán trên, mọi người có thể xem qua ví dụ ngay sau đây:
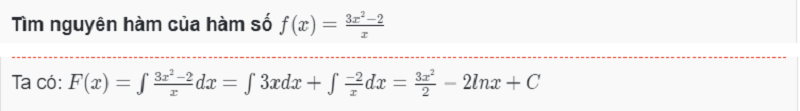
Tìm nguyên hàm của hàm số hữu tỉ bằng phương pháp đồng nhất thức
Dạng toán tìm nguyên hàm số hữu tỉ dựa vào phương pháp đồng nhất thức khá hiệu quả mà các em có thể áp dụng theo các bước sau:
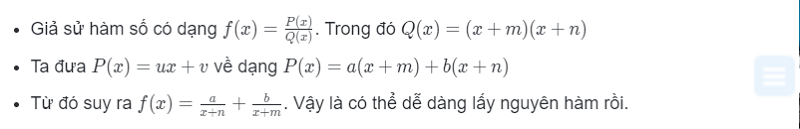
Dưới đây là ví dụ tham khảo giúp học sinh hiểu rõ hơn về dạng toán này và phương pháp giải.
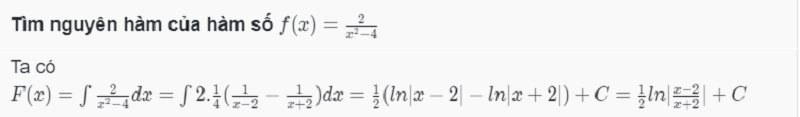
Tìm nguyên hàm của hàm số hữu tỉ bằng phương pháp đưa về dạng lượng giác
Đối với các dạng toán tìm nguyên hàm hàm số hữu tỉ không thể áp dụng được theo hai phương pháp trên, mọi người có thể chuyển sang cách đưa dạng đó về dạng lượng giác. Rồi từ đó áp dụng công thức tính nguyên hàm để lấy nguyên hàm của chính hàm số hữu tỉ đó.
Dưới đây là ví dụ minh họa về phương pháp tìm nguyên hàm số hữu tỉ đưa về dạng lượng giác cơ bản sau:

Một số bài tập tự luyện về nguyên hàm hữu tỉ
Sau khi đã nắm rõ được các khái niệm, công thức, dạng bài tập liên quan tới nguyên hàm của hàm số hữu tỉ, dưới đây là một số bài tập thực hành để học sinh có thể tham khảo, luyện tập và ứng dụng:

Tìm hiểu thêm: Nguyên hàm hàm hợp là gì? Công thức và cách giải nguyên hàm của hàm hợp như thế nào?
Kết luận
Trên đây là tổng hợp những kiến thức cơ bản về toán nguyên hàm hữu tỉ. Qua đó có thể nhận thấy được đây là một dạng toán có nhiều kiến thức quan trọng mà học sinh cần nhớ, nhất là việc nắm rõ công thức, dạng toán và cách giải. Hy vọng dựa vào những chia sẻ trên của Wikihoc, các em sẽ dễ dàng chinh phục được bài tập nguyên hàm này tốt hơn nhé.
