Đạo hàm lượng giác là một trong những phần học chính của chương trình giải tích lớp 11. Kiến thức đạo hàm này sẽ khá phức tạp và khó hiểu nếu học sinh không nắm vững được những nội dung cơ bản ngay từ buổi đầu.
Do đó, với bài viết tổng hợp đầy đủ lý thuyết về khái niệm, các công thức tính và mẫu bài tập dưới đây, Wikihoc hy vọng có thể giúp bạn ôn lại kiến thức đạo hàm lượng đã học một cách hiệu quả hơn.
Đạo hàm là gì? Các công thức tính đạo hàm cơ bản
Khái niệm đạo hàm
Đầu tiên, trước khi giải bất kỳ bài toán cơ bản hay nâng cao nào, chúng ta cần hiểu thật rõ khái niệm về đạo hàm. Theo đó, trong phạm trù vật lý học, đạo hàm được hiểu là sự mô phỏng vận tốc tức thời của một điểm chuyển động bất kỳ hoặc cường độ tức thời của dòng điện tại một điểm trên đoạn dây dẫn.
Còn ở phương diện toán học, đạo hàm đóng góp ý nghĩa cả phần hình học lẫn giải tích. Cụ thể, trong toán hình, khái niệm đạo hàm chính là hệ số góc giữa tiếp tuyến và đồ thị khảo sát hàm số đã cho. Và tại nội dung giải tích chúng ta sẽ tìm hiểu ở bài viết này, đạo hàm được định nghĩa rất chi tiết như sau:
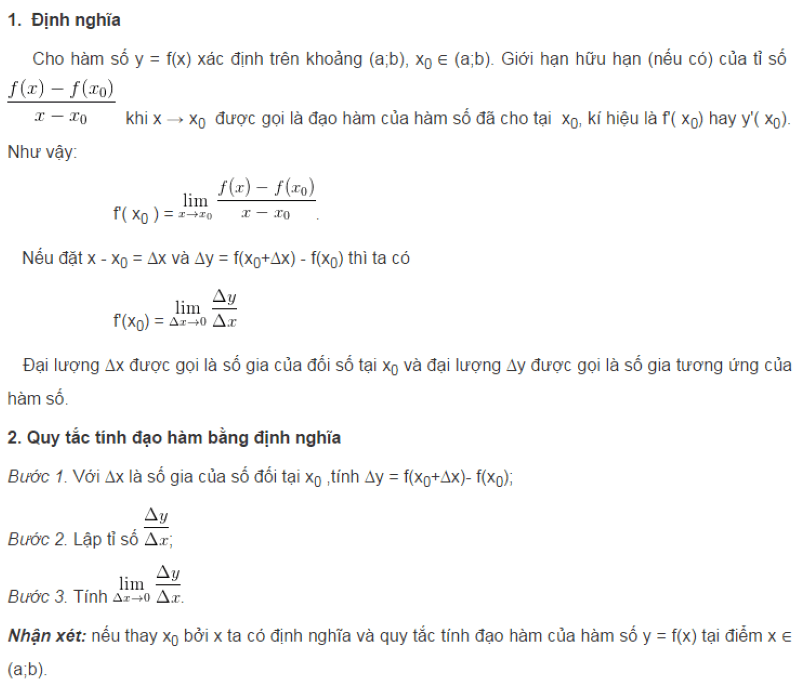
Tổng hợp công thức tính đạo hàm
Dựa vào định nghĩa và cách tính đạo hàm cơ bản như trên, học sinh chắc hẳn đã hiểu rõ được thế nào là đạo hàm. Vậy, tiếp theo, chúng mình cùng đến với phần kiến thức khó hơn cũng như đòi hỏi khả năng ghi nhớ cao hơn ở các bạn.
Đó chính là bảng công thức được áp dụng nhiều nhất trong khi giải bài tập tính đạo hàm. Hãy xem đó là những công thức tính đạo hàm nào nhé!

Vì đây là những công thức tính đạo hàm cơ bản nên các bạn học sinh nhớ chú ý học thật kỹ và ghi nhớ chính xác để sử dụng trong khi giải bài tập. Một bí quyết Wikihoc mách đến bạn, đó là mỗi ngày hãy dành từ 30 phút đến 1 tiếng để làm đi làm lại một dạng bài với cùng một công thức được áp dụng, cho đến khi hình thành nên thói quen và tự động ghi ra được công thức mà không cần xem lại trong sách vở. Như vậy, bạn đã biết thêm một phương pháp học công thức tính đạo hàm rất dễ dàng mà hiệu quả đem đến lại cực cao rồi đấy.
Xem thêm: Thế nào là đạo hàm lượng giác? Chi tiết cách giải bài tập đạo hàm lượng giác thường gặp
Đạo hàm lượng giác là gì? Bảng công thức tổng hợp các đạo hàm lượng giác
Đạo hàm hàm lượng giác được hiểu là các bài toán đi tìm sự biến thiên của một hàm số lượng giác dựa trên tốc độ biến thiên của biến số. Trong đó, các hàm số lượng giác thường gặp nhất là hàm sin(x), tan(x), và cos(x).
Dựa vào đây, ta có các công thức đã được xây dựng và chứng minh để giúp quá trình tính đạo hàm lượng giác dễ dàng, nhanh chóng hơn. Wikihoc sẽ cung cấp đến bạn một bảng công thức đầy đủ dưới đây.
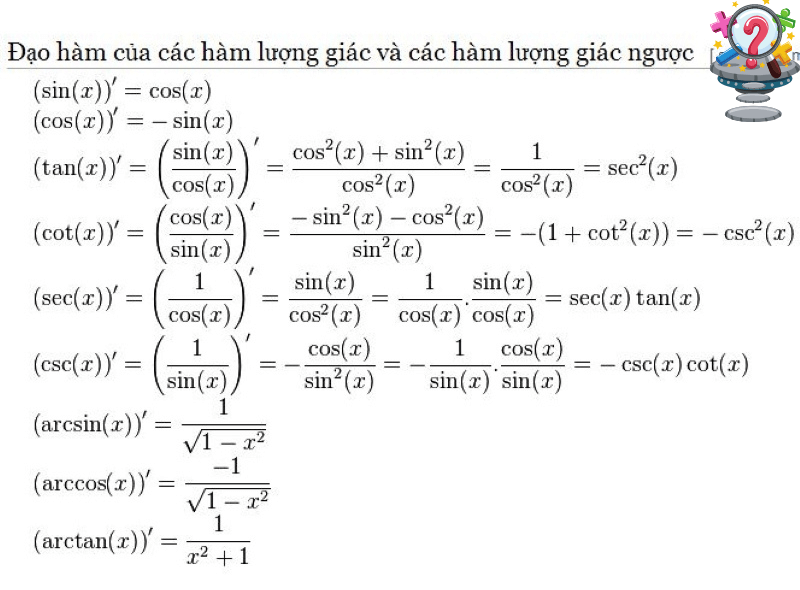
Với các công thức đạo hàm hàm lượng giác này, học sinh chỉ cần học thuộc và được phép đưa ngay vào áp dụng trong các dạng bài tập mà không cần chứng minh. Nhờ đây, bạn sẽ bớt được nhiều bước biến đổi và rút gọn đáng kể thời gian để giải ra một câu tính đạo hàm lượng giác.
Cách tính đạo hàm lượng giác có mũ đơn giản nhất
Đạo hàm của hàm lượng giác có mũ là một dạng công thức cấp cao trong giải tích. Phần kiến thức này thường được đưa vào các câu thuộc thang điểm 8-9 trong bộ đề THPT Quốc Gia.
Do đó, nếu học sinh chinh phục được những công thức khó nhằn này thì sẽ thật đơn giản để có một số điểm như mong đợi. Vậy, ngay sau đây, chúng mình cùng nhau lướt xem bảng đạo hàm lượng giác có mũ và ghi nhanh ra giấy để học thuộc bạn nhé!
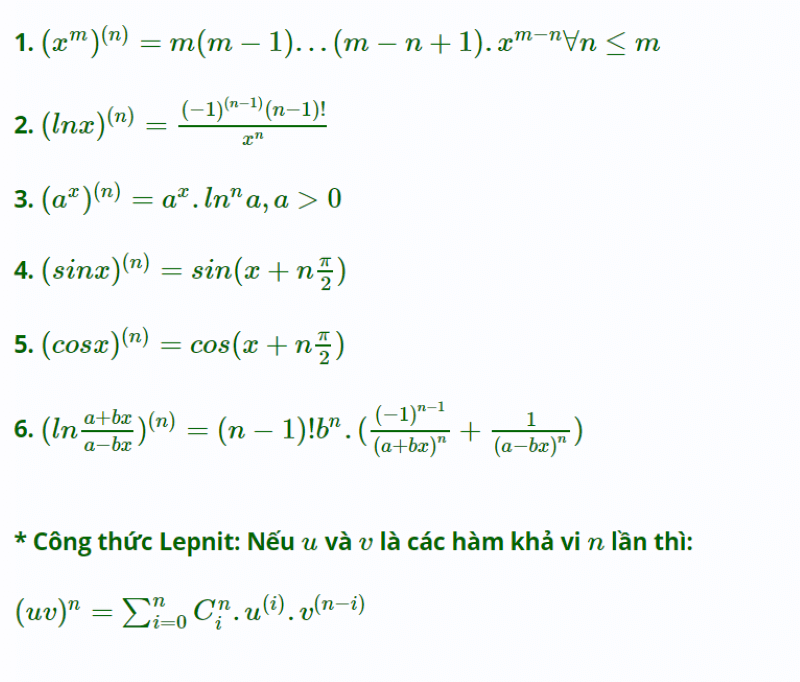
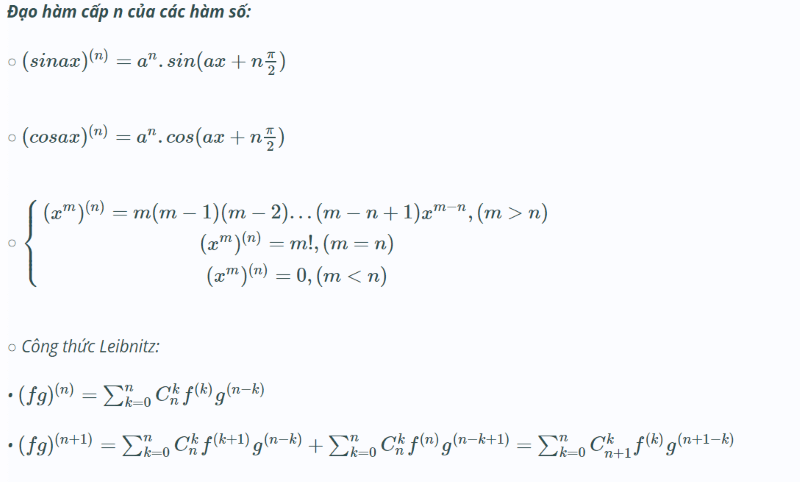
Một số dạng bài tập đạo hàm lượng giác thường gặp có lời giải
Khi học các công thức tính đạo hàm lượng giác bên trên, nó không đơn giản chỉ là ghi nhớ và học thuộc lòng. Mà học sinh cần biết áp dụng công thức sao cho thích hợp với từng kiểu bài tập để có được cách giải nhanh và đơn giản nhất.
Cũng do đó, song song với việc nắm chắc các cách biến đổi của đạo hàm lượng giác lớp 11, bạn còn cần biết những dạng bài tập thường gặp và phương pháp giải chi tiết nhất. Đối với hàm lượng giác, các mẫu bài cơ bản bao gồm như sau:
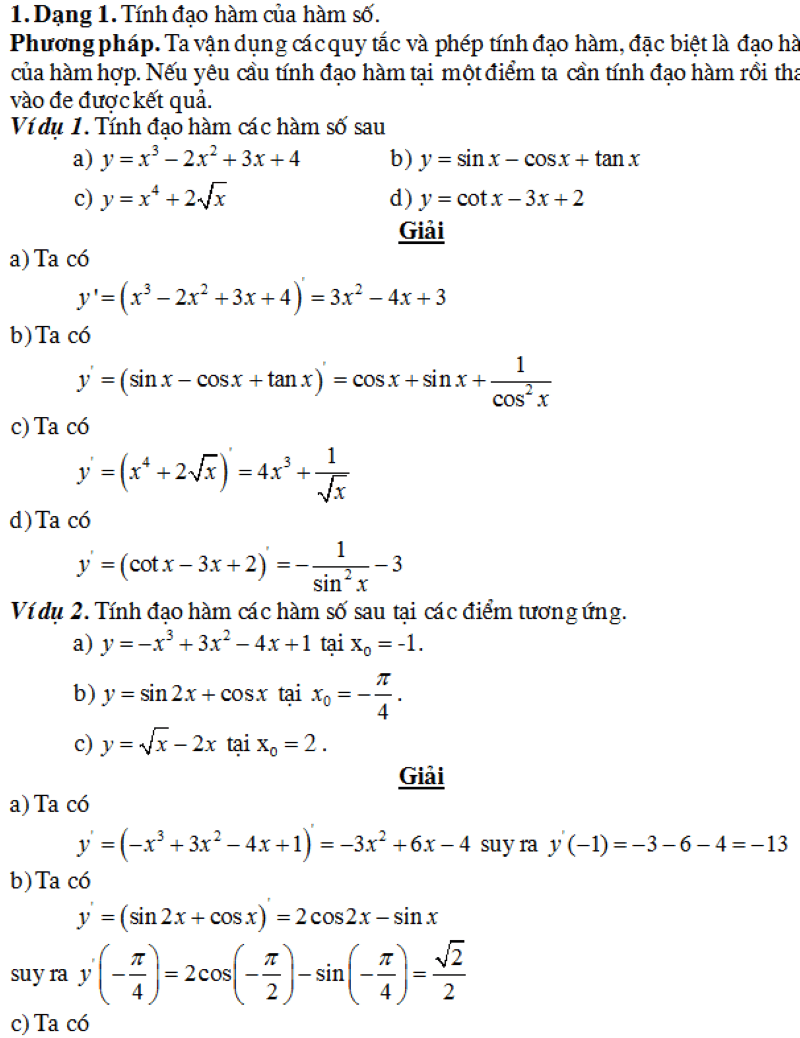
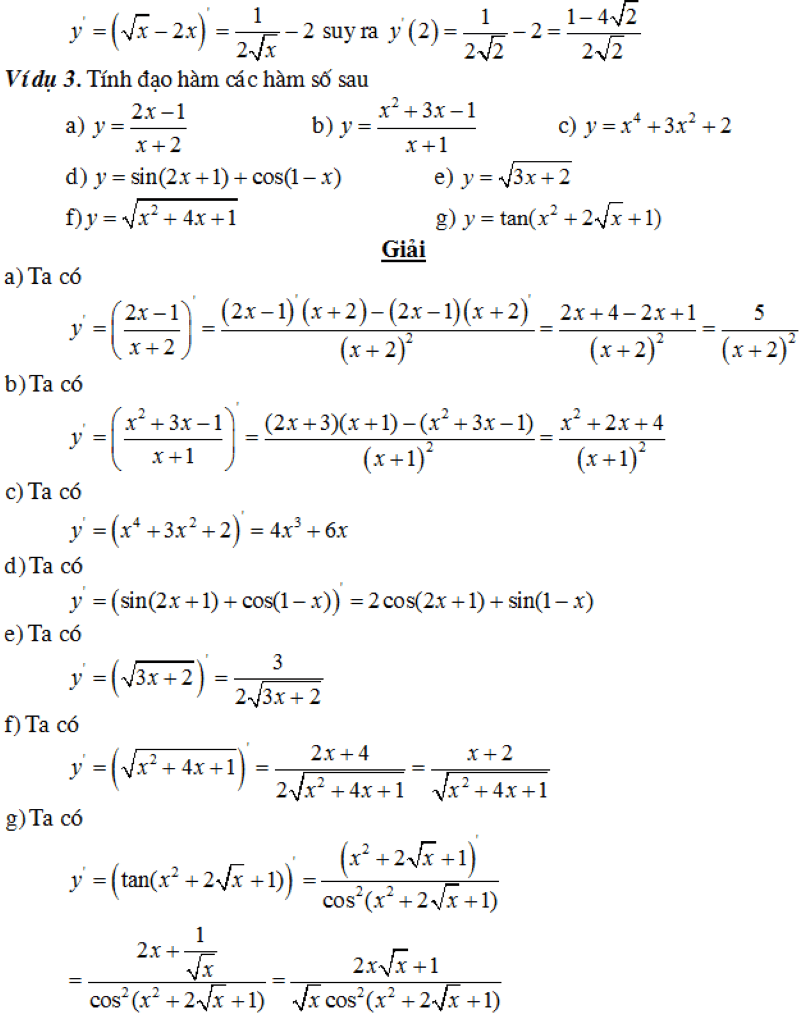


Một số mẹo giúp giải nhanh các bài toán đạo hàm lượng giác
Chắc hẳn nhiều bạn sau khi đọc xong phần kiến thức trên đang cảm thấy vô cùng áp lực và chán nản vì lượng lớn cách tính đạo hàm lượng giác cần ghi nhớ. Thế nhưng, đừng lo lắng quá nhiều nhé, vì ngay sau đây, Wikihoc sẽ chỉ cho học sinh những bí quyết đặc biệt để việc học đạo hàm không còn là khó khăn.
Cách 1: Ghi chú ra giấy nhớ hoặc sổ tay học tập
Đây có thể nói là một phương pháp học rất truyền thống. Tuy nhiên, Wikihoc vẫn liệt kê vào danh sách những “mẹo” hay bởi tính hiệu quả mà cách học này đem lại.
Đầu tiên, bằng trí sáng tạo của mình, học sinh hãy tự trang trí cho cuốn sổ công thức bằng những màu sắc hoặc hình ảnh thật ngộ nghĩnh, bắt mắt. Bởi điều này sẽ giúp kích thích trí não và tinh thần học tập lên cao hơn cũng như duy trì sự tỉnh táo khi phải nhìn vào sách vở trong một thời gian dài.
Còn nếu bạn lựa chọn ghi công thức đạo hàm lượng giác ra giấy ghi chú, hãy chọn mua tệp note dễ thương của những nhân vật hoạt hình bạn yêu thích và dán đầy góc học tập. Nhờ đó, các đạo hàm lượng giác sẽ xuất hiện trong tầm nhìn ngay khi học sinh ngồi xuống bàn học. Và giúp bạn có thể nhẩm học các công thức ở mọi lúc đấy. Hãy thử áp dụng ngay phương pháp hay ho này cùng Wikihoc nhé.
Cách 2: Học công thức vào sáng sớm
Buổi sáng sớm là thời điểm vô cùng lý tưởng để ôn tập và học thuộc các kiến thức quan trọng, đặc biệt là đạo hàm lượng giác. Bởi lúc này, các cơ quan được nghỉ ngơi và điều tiết đầy đủ, nên sẽ tràn đầy năng lượng để ghi nhớ sâu và bật ra nhiều ý tưởng mới.
Do đó, ngoài việc dành thời gian buổi sáng học thuộc công thức, học sinh cũng có thể kết hợp làm thêm các bài tập đạo hàm hàm lượng giác dạng nâng cao. Hãy duy trì thói quen này mỗi sáng và bạn sẽ phải bất ngờ với những kết quả tích cực có được đấy.
Cách 3: Học nhiều lần một công thức
Phương pháp này đòi hỏi ở người học sự kiên trì và nhẫn nại vô cùng lớn. Bởi dành nhiều thời gian để ôn tập một công thức có thể làm bạn thấy nhàm chán và nản lòng. Thế nhưng, nếu bạn chưa thuộc sâu và hiểu kỹ công thức đạo hàm lượng giác bất kỳ mà đã chuyển sang học các hàm khác thì khi làm bài sẽ rất khó để áp dụng một cách linh hoạt.
Vì vậy, các bạn nên học đi học lại một hàm lượng giác cho đến khi thật thành thạo và không còn mất công giở sách để tìm lại công thức. Đây được biết đến là một mẹo học đơn giản mà lại rất hiệu quả cho mọi học sinh chúng mình đấy.
Trên đây, Wikihoc đã gửi tới bạn đọc các kiến thức từ cơ bản đến nâng cao của đạo hàm lượng giác. Hy vọng, với những lời nhắn nhủ được gửi gắm trong bài viết, học sinh sẽ có thêm thật nhiều động lực để chăm chỉ ôn tập mỗi ngày và đạt được kết quả tốt nhất nhé.
