Chu vi hình tam giác cũng sẽ có nhiều công thức khác nhau tùy thuộc vào loại hình tam giác. Chính vì vậy, để giúp các em nắm bắt và ghi nhớ được công thức tính chu vi của các loại hình tam giác cân, đều, vuông, nhọn hãy cùng Wikihoc tham khảo bài viết sau đây nhé.
Tại sao cần tính chu vi tam giác
Khi nắm được kiến thức hình tam giác là gì? Chắc hẳn mọi người cũng biết được, việc nắm được công thức tính toán của hình từ diện tích tam giác cho đến chu vi đều rất quan trọng.

Điển hình như công thức tính chu vi, khi nắm rõ sẽ giúp bé giải quyết được các bài tập liên quan trong chương trình học. Đồng thời, kiến thức này cũng được vận dụng trong thực tế cuộc sống hàng ngày để tính toán các vật thể tam giác thực.
Công thức tính chu vi hình tam giác
Dựa vào tính cách các cạnh, các góc, chiều cao nên tùy vào từng hình tam giác sẽ có công thức tính chu vi khác nhau. Cụ thể:

Tính chu vi tam giác thường
Tam giác thường là hình tam giác với 3 cạnh có độ dài khác nhau, với công thức tính chu vi như sau:
P = a + b + c
Trong đó:
-
P là chu vi tam giác.
-
a, b, c là 3 cạnh của hình tam giác đó.
Để tính nửa chu vi tam giác sẽ dựa theo công thức: ½P = (a+b+c) : 2
Ví dụ: Cho tam giác có độ dài 3 cạnh lần lượt là 5cm, 7cm và 10cm. Tính chu vi hình tam giác.
Dựa vào công thức chúng ta sẽ có lời giải là P = 5 + 7 + 10 = 22cm
Đáp án: chu vi tam giác bằng 22cm.
Tính chu vi tam giác cân
Tam giác cân là hình tam giác với 2 góc và 2 cạnh bằng nhau. Trong đó, đỉnh tam giác cân chính là giao điểm của 2 cạnh bên. Chính vì vậy, để tính được chu vi tam giác cân, mọi người sẽ phải biết được chính xác độ dài 2 cạnh bên là được.
Công thức tính như sau:
P = 2a + c
Trong đó:
-
a: Hai cạnh bên của tam giác cân.
-
c: Là đáy của tam giác.
Lưu ý: Với công thức tính chu vi tam giác cân này, cũng có thể áp dụng để tính chu vi tam giác vuông cân.
Ví dụ: Cho hình tam giác cân tại A với chiều dài AB = 9cm, BC = 12cm. Tính chu vi hình tam giác cân.
Dựa vào công thức tính chu vi tam giác cân, ta có cách tính P = 2 x 9 + 5 = 23cm.
Tính chu vi tam giác đều
Tam giác đều là tam giác với 3 cạnh bằng nhau. Công thức tính chu vi của chúng sẽ là:
P = 3 x a
Trong đó
-
P: Là chu vi tam giác đều.
-
a: Là chiều dài cạnh của tam giác.
Ví dụ: Tính chu vi tam giác đều có cạnh AB = 7cm.
Dựa theo công thức chúng ta có cách tính P = 3 x 7 = 21cm.
Tính chu vi tam giác vuông
Tam giác vuông là hình tam giác với 1 góc vuông bằng 90°. Công thức tính chu vi của hình sẽ là:
P = a + b + c
Trong đó
-
a và b: Hai cạnh của tam giác vuông.
-
c: Cạnh huyền của tam giác vuông.
Ví dụ: Tính chu vi tam giác vuông với độ dài CA = 5cm, CB = 8cm và AB = 12cm.
Dựa vào công thức tính chúng ta có cách tính P = 5 + 8 + 12 = 25cm.
Với tam giác vuông, ta có thể tính chu vi khi biết độ dài 2 cạnh.
Ví du: cho tam giác vuông ABC, với cạnh CA = 5cm, CB = 8cm, tính chu vi.
Lúc này, AB là cạnh huyền vuông ở C. Nên để tính cạnh huyền tam giác vuông ta, áp dụng định lý Pitago để tính như sau:
AB² = CA² + CB²
AB² = 25 + 64
AB = 9,4cm
Vậy chu vi tam giác vuông CAB là:
P = 5 + 8 + 9,4 = 22,4cm
Công thức tính chu vi tam giác trong không gian
Giả sử, ở bài toán tính chu vi tam giác trong không gian với mặt phẳng Oxy, ta có 2 điểm với tọa độ A(1;3), B(4;2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA=DB;
b) Tính chu vi tam giác OAB?
Lời giải:
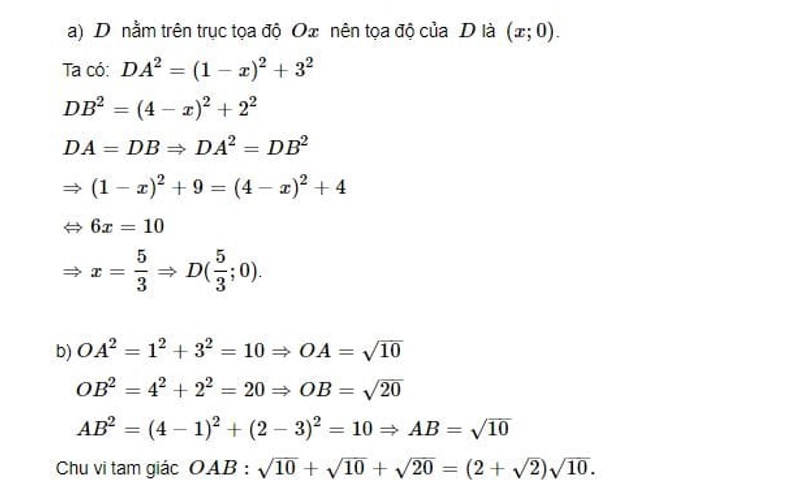
Bài tập toán tính chu vi hình tam giác để bé luyện tập
Sau khi đã nắm được công thức tính chu vi của các hình tam giác, dưới đây là tổng hợp một số bài tập liên quan để các em có thể áp dụng, thực hành hiệu quả:

Bí quyết giúp bé học, ghi nhớ kiến thức chu vi hình tam giác hiệu quả
Đối với các bé học lớp 1, thường kiến thức về chu vi của hình tam giác ở mức cơ bản, chưa có nhiều dạng toán khó. Nhưng để đảm bảo trẻ ghi nhớ, hiểu và áp dụng khi giải bài tập hay thực hành trong thực tế hiệu quả, bố mẹ hãy tham khảo một số bí quyết sau đây:
Xây dựng nền tảng toán học vững chắc từ sớm cho trẻ với Wikihoc Math
Wikihoc Math được biết đến là ứng dụng học toán tiếng Anh cho trẻ mầm non và tiểu học do Wikihoc phát triển.
Trong đó, nội dung bài học của Wikihoc Math phát triển đều bám sát theo chương trình GDPT mới mà Bộ GDĐT đưa ra, kết hợp cùng với chương trình toán tiếng Anh chuẩn Mỹ. Điều này hoàn toàn phù hợp với đa số định hướng giáo dục hiện đại của bố mẹ dành cho trẻ.
Đồng thời, khi con theo học cùng Wikihoc Math sẽ dễ dàng theo học các trường quốc tế. Còn với các bé học trường công, Wikihoc Math cũng là một công cụ hoàn hảo để trẻ được trang bị nền tảng tốt để tiếp thu bài vở trên lớp hiệu quả hơn.
Đặc biệt, với Wikihoc Math, không chỉ đơn thuần là việc cung cấp kiến thức toán học, phương pháp giải toán mà còn giúp bé hiểu được bản chất cốt lõi của từng bài học. Ở đây, bé sẽ hiểu rõ về lượng về chất thay vì chỉ học vẹt đơn thuần.
Qua đó, dần dần sẽ giúp con rèn luyện được tư duy giải quyết vấn đề, cũng như hình thành được khả năng tư duy logic ngay từ nhỏ. Hay thay vì được học lý thuyết, con sẽ được ứng dụng kiến thức đã được học vào giải quyết vấn đề thực tế như xem đồng hồ, nhận biết hình học, tính chu vi tam giác qua ví dụ, so sánh…

Với Wikihoc Math sẽ có khoảng hơn 400 bài học, 10.000+ hoạt động tương tác dựa trên 60+ chủ đề toán học của 7 chuyên đề toán chính. Để qua đó con sẽ vừa được học tập vui vẻ, tiếp thu toán một cách tự nhiên cũng như giúp các bài học ngấm sâu, nhớ lâu hơn khi con học bằng các giác quan:
-
Thị giác – quan sát, nhìn.
-
Thính giác – nghe.
-
Xúc giác – các hoạt động tương tác trực tiếp (vận động tinh, vận động thô).
Đảm bảo, sau khi học cùng Wikihoc Math, con sẽ vừa được chơi, vừa được học và tiếp thu toán dễ dàng. Từ đó con sẽ yêu thích toán và tự giác học tập hơn mà không cần bố mẹ nhắc nhở.
Cùng như, với Wikihoc Math bé còn vừa được học toán, vừa được luyện học tiếng Anh một cách tự nhiên. Đây là những kiến thức quan trọng để bổ trợ rất tốt cho việc học tập của bé ở hiện tại và tương lai.
Đảm bảo bé nắm vững kiến thức cơ bản khi học tính chu vi hình tam giác
Để có thể giải quyết được các bài tập toán học nói chung, bài tập tính chu vi của hình tam giác nói riêng đòi hỏi các em phải nắm vững các kiến thức cơ bản. Điển hình như hình tam giác là gì? Các loại hình tam giác, công thức tính chu vi, diện tích của từng hình,…
Đặc biệt, để biết được bé đã nắm vững kiến thức hay chưa, bố mẹ nên kiểm tra năng lực học của con thông qua việc xem sách vở, bài tập của trẻ. Bên cạnh đó, có thể đặt ra những câu hỏi liên quan như công thức tính tam giác vuông như thế nào? Nêu ví dụ về bài tập tính chu vi tam giác bất kỳ?… Để qua đó bạn biết được bé đang yếu phần nào để bổ sung, củng cố kịp thời cho trẻ hiệu quả.
Học kết hợp với thực hành là điều không thể thiếu
Đây là một trong những yếu tố quan trọng trong quá trình học tập hay làm việc không thể bỏ qua. Bởi vì nếu chỉ nắm vững lý thuyết mà không thực hành thường xuyên rất dễ nhanh quên, cũng như không biết cách ứng dụng vào thực tế khi gặp bài toán, vấn đề.

Vậy nên, với kiến thức tính chu vi tam giác cũng không ngoại lệ, bố mẹ cũng cần phải cùng con làm các bài tập trong SGK, Wikihoc Math, đề thi,… cho đến việc tìm hiểu thêm nhiều kiến thức mới trên internet, cùng bạn bè học nhóm, tổ chức các trò chơi, câu đố,… để từ đó con được thực hành, luyện tập nhiều hơn rất tốt cho việc phát triển kiến thức và tư duy giải quyết vấn đề của trẻ.
Kết luận
Trên đây là tổng hợp những thông tin kiến thức về cách tính chu vi hình tam giác. Đây đều là những kiến thức nền tảng quan trọng hỗ trợ việc học của bé trên trường, cũng như trong đời sống tốt hơn. Nên bố mẹ hãy cùng con tham khảo và áp dụng để giúp bé phát triển năng lực học tập tốt hơn nhé.
