Hai đường thẳng song song là kiến thức cơ bản trong toán hình học cần nắm vững, vì nó có liên quan tới nhiều kiến thức nâng cao hơn khi giải bài tập. Vậy nên, để hiểu rõ hơn về kiến thức này, hãy cùng Wikihoc tìm hiểu chi tiết ngay trong bài viết sau đây nhé.
Hai đường thẳng song song là gì?
Hai đường thẳng song song trong một mặt phẳng chính là hai đường thẳng không có điểm chung.
Kí hiệu a//b.
Trong hình học, hai đường thẳng phân biệt thì hoặc cắt nhau hoặc song song.
Dấu hiệu nhận biết 2 đường thẳng song song
Dưới đây là một số dấu hiệu nhận biết hai đường thẳng song song:
-
Trong một mặt phẳng, nếu 2 đường thẳng cắt một đường thẳng thứ 3 tạo thành cặp góc so le bằng nhau thì đó là 2 đường thẳng song song.
-
Nếu 2 đường thẳng cắt một đường thẳng thứ 3 tạo thành cặp góc đồng vị bằng nhau thì 2 đường thẳng song song.
-
Nếu 2 đường thẳng cắt một đường thẳng thứ 3 tạo thành cặp góc trong cùng phía bù nhau thì 2 đường thẳng song song.
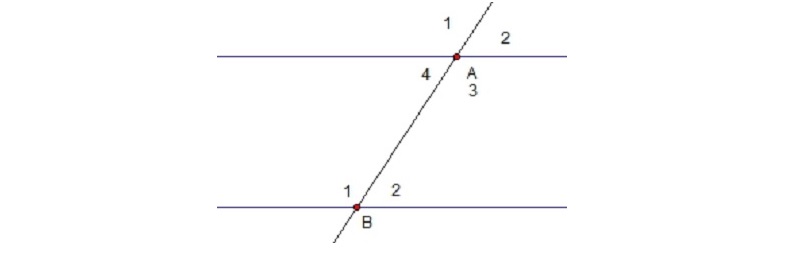
Ví dụ: trong hình vẽ, C là đoạn thẳng AB.
Đặc điểm tính chất của hai đường thẳng song song
Trong một mặt phẳng, nếu 2 đường thẳng song song bị cắt bởi đường thẳng thứ 3 thì:
-
Hai góc so le trong còn lại bằng nhau
-
Hai góc đồng vị bằng nhau
-
Hai góc trong cùng phía bù nhau
-
Qua một điểm nằm ngoài một đường thẳng, chỉ có một đường thẳng song song song với đường thẳng đó.
Cách vẽ 2 đường thẳng song song với nhau
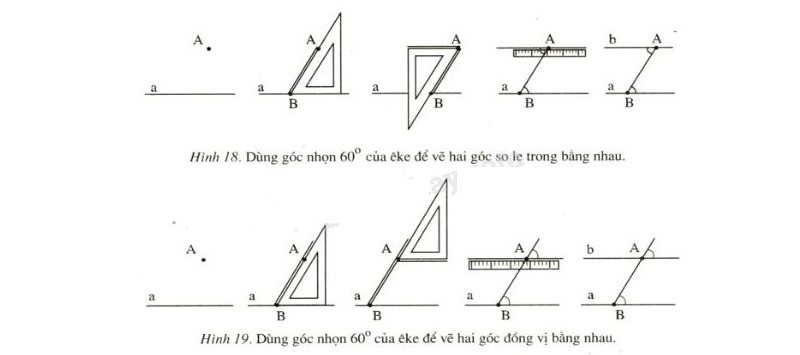
Để có thể vẽ được 2 đường thẳng song song chính xác, ta có thể dùng thướng eke hoặc thước thẳng để vẽ. Cụ thể như sau:
Các dạng toán về 2 đường thẳng song song thường gặp
Trong chương trình toán học lớp 4, với phần hình học các em sẽ được làm quen với những dạng bài tập liên quan tới hai đường thẳng song song như sau:
Dạng 1: Vẽ đường thẳng song song theo yêu cầu
Phương pháp giải: Các em sẽ dựa vào hướng dẫn cách vẽ 2 đường thẳng song song trên kết hợp với yêu cầu đề bài đưa ra để tiến hành vẽ chính xác.
Ví dụ:
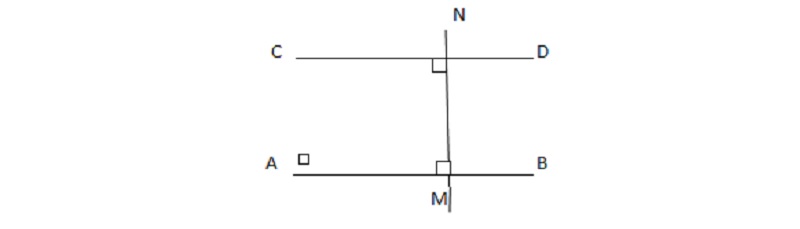
Hãy vẽ đường thẳng AB đi qua điểm M và song song với đường thẳng CD
Hướng dẫn giải:
- Bước 1: Vẽ đường thẳng MN đi qua M và vuông góc với CD
- Bước 2: Vẽ đường thẳng AB đi qua M và vuông góc với MN
Dạng 2: Nhận biết và chứng minh hai đường thẳng song song
Phương pháp giải: Ta sẽ dựa vào đặc điểm tính chất cùng dấu hiệu nhận biết 2 đường thẳng song song để nhận biết và chứng minh theo yêu cầu.
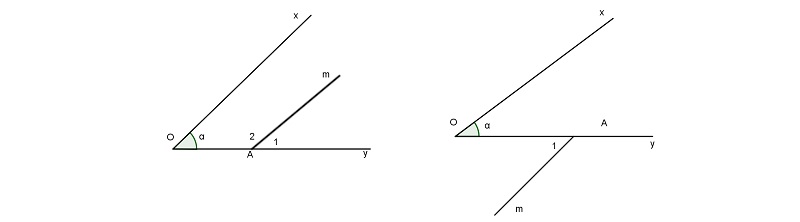
Ví dụ: Cho góc xOyˆ=α, điểm A nằm trên tia Oy. Qua điểm A vẽ tia Am. Tính số đo OAmˆ để Am song song Ox.
Hướng dẫn giải:
Ta xét hai trường hợp:
Nếu tia Am thuộc miền trong xOyˆ:
Để Am//Ox thì ta phải có A1ˆ=α (đồng vị)
Mà A1ˆ+A2ˆ=180∘ (kề bù)
Suy ra A2ˆ=180∘−A1ˆ=180∘−α
Vậy OAmˆ=180∘−α
Nếu tia Am thuộc miền ngoài xOyˆ:
Để Am//Ox thì ta phải có A1ˆ=α (so le trong)
Vậy OAmˆ=α
Dạng 3: Tính số đo góc
Phương pháp giải: Dựa vào tính chất và dấu hiệu nhận biết của 2 đường thẳng song song, kết hợp với phép tính toán thông thường để tính số đo góc chính xác.
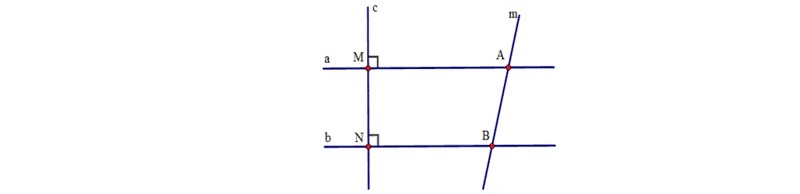
Ví dụ: Cho đường thẳng a và đường thẳng b cùng vuông góc với đường thẳng c, c vuông góc với a tại điểm M và vuông góc với b tại điểm N. Một đường thẳng m cắt a, b tại điểm A và điểm B. Biết góc (ABN – MAB) = 40°. Số đo góc BAM là bao nhiêu?
Hướng dẫn giải:
Từ đề bài đã cho ta có: a ⊥ c, b ⊥ c ⇒ a // b
⇒ ∠ABN + ∠MAB = 180° (hai góc trong cùng phía bù nhau)
Dạng 4: Xác định các góc bù hoặc bằng nhau dựa vào tính chất hai đường thẳng song song
Phương pháp giải: Đầu tiên, các em sẽ phải chứng minh 2 đường thẳng đó song song (nếu chưa có), sau đó dựa vào tính chất của chúng để giải bài tập chính xác.
Ví dụ:
Đề bài cho ba đường thẳng phân biệt a, b, c biết a // b và a ⊥ c. Kết luận nào là đúng:
A. b // c
B. b ⊥ c
C. a ⊥ b
D. Tất cả các đáp án đều sai
Hướng dẫn giải
Ta có:
Chọn đáp án B.
Bí quyết học và ghi nhớ kiến thức hai đường thẳng song song hiệu quả
Đối với kiến thức 2 đường thẳng song song tưởng chừng như đơn giản, nhưng càng học về sau sẽ càng khó. Vậy nên, để giúp các em nắm rõ được kiến thức cơ bản này chắc chắn hơn thì dưới đây là một số bí quyết để mọi người tham khảo:
Học và ghi nhớ lý thuyết hai đường thẳng //
Để có thể chinh phục được các bài tập từ cơ bản đến nâng cao, đòi hỏi các em phải học và nắm rõ được lý thuyết của dạng toán này. Nhất là khái niệm, dấu hiệu nhận biết, đặc điểm và tính chất của 2 đường thẳng //.
Đồng thời, bố mẹ cũng cần giải thích rõ từng phần mà bé chưa hiểu, lấy ví dụ cụ thể cho đến khi bé hiểu và ghi nhớ chúng.
Ngoài ra, bạn cũng nên thường xuyên kiểm tra lại kiến thức cũ, để tránh trường hợp bé học trước quên sau. Cũng như củng cố kiến thức kịp thời nếu như con quên để tránh trường hợp khi học thêm nhiều kiến thức mới bé khó học lại bài cũ.

Học đi đôi với hành là điều không thể thiếu
Sau khi con đã nắm và hiểu được rõ lý thuyết về hai đường thẳng song song. Bố mẹ nên tạo cơ hội để con được thực hành nhiều hơn. Bởi nếu chỉ học lý thuyết các con sẽ rất nhanh quên, nhưng khi được thực hành thường xuyên sẽ tăng khả năng ghi nhớ, tư duy để làm bài tập chính xác.
Việc thực hành ở đây có thể áp dụng như cùng con làm bài tập trên trường, SGK, sách bài tập, sưu tầm thêm nhiều kiến thức mới trên internet, tham khảo nhiều bài tập nâng cao….
Trang bị đầy đủ dụng cụ học tập cho bé
Trong toán học nói chung, hình học nói riêng để giúp bé học tốt hơn bố mẹ nên đầu tư các bộ dụng cụ học tập. Điển hình nhất là bộ thước kẻ từ kẻ thẳng, eke, thước đo góc… để giúp việc vẽ đường thẳng, vẽ hình, đo góc một cách chính xác hơn.

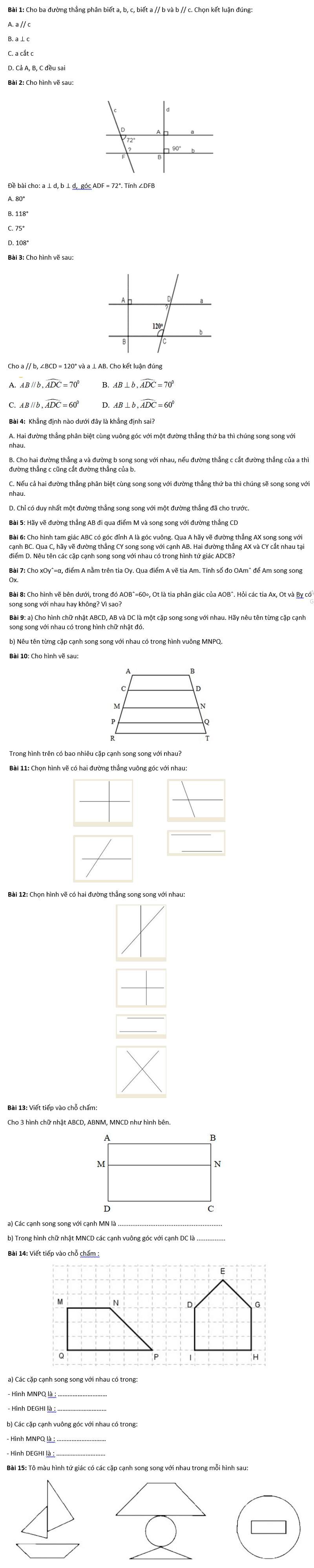
Một số bài tập về 2 đường thẳng song song để bé luyện tập
Dưới đây là một số bài tập liên quan tới hai đường thẳng // để các em cùng nhau luyện tập nhé.
Kết luận
Trên đây là những thông tin kiến thức cơ bản về hai đường thẳng song song. Đây chính là nền tảng quan trọng để hỗ trợ việc học toán hình của bé tốt hơn. Hy vọng với những gợi ý trên sẽ giúp việc học tập của bé đạt kết quả tốt hơn.
